I'm quite a newbie in differential geometry. Calculus is not my cup of tea ; but I find geometrical proofs really beautiful. So I'm looking for a simple - by simple I mean with almost no calculus - proof that the shortest path between two points on a sphere is the arc of the great circle on which they lie. Any hint ?
Edit: Or at least a reference ?
Here's a geometric observation that can hardly be called a "proof", but may be appealing nonetheless.
If $p$ and $q$ are distinct points of the sphere $S^{n}$, if $C:[0, 1] \to S^{n}$ is a "shortest path" joining $p$ to $q$, and if $F:S^{n} \to S^{n}$ is a distance-preserving map fixing $p$ and $q$, then $F \circ C$ is also a shortest path (because the length of $F \circ C$ is equal to the length of $C$).
Assume $q \neq -p$. If you believe there exists a unique shortest path from $p$ to $q$, it's not difficult to see that the "short" great circle arc is the only candidate: Every point not on the great circle through $p$ and $q$ is moved by some isometry of the sphere that fixes $p$ and $q$.
If you're thinking specifically of $S^{2}$, reflection $F$ in the plane containing $p$, $q$, and the center of the sphere is an isometry, and $f(x) = x$ if and only if $x$ lies on the great circle through $p$ and $q$.
(A similar argument "justifies" that the shortest path between distinct points of the Euclidean plane is the line segment joining them.)
You can show that great circle arcs are geodesics by parameterizing such an arc so that it has unit speed, and then showing that the acceleration along the arc is perpendicular to the sphere surface. (This assumes you accept that geodesics have the characteristic that their acceleration is perpendicular to the tangent plane of the surface at each point of the geodesic.)
Then uniqueness of the geodesic from a point in a direction shows it must be the great circle arc.
I realize this might not be what you seek because it doesn't connect directly to shortest paths...
(parallel symmetry) Consider the plane that is the perpendicular bisector of the straight line segment joining the two points. All objects (i.e., the sphere and the points) are symmetric with respect to that plane, so if the path is unique, it must stay the same after it is reflected across the plane.
Why? Because otherwise it wouldn't be unique -- by reflecting the problem, we would be keeping the inputs the same, but changing the output, and hence the path wouldn't be a function of the inputs.
(perpendicular symmetry) Now consider the plane of the great circle -- that is, the plane that goes through the center of the sphere as well as the two given points. Again, the sphere and the points are reflectively symmetric with respect to this plane, so if the path is unique, it must stay the same after being reflected across this plane. (Same reason as above.)
(spherical constraint) The path must, by definition of the problem, lie on the sphere.
(uniqueness) The path must be unique. (This is intuitively obvious, so I won't try to prove it.)
It's easy to see that the only path that satisfies these three conditions is the one on the great circle.
Why? Because the intersection of the sphere with the two planes of symmetry clearly satisfies conditions 1-3. Furthermore, condition 4 implies that no other path can be the shortest path. Hence, the intersection of these shapes must be the shortest path itself.
This method only works for this problem. By contrast, calculus-based methods (see the Calculus of Variations) work for other problems that lack such symmetries, and hence you should still learn those approaches so you can solve the shortest path problem for e.g. ellipsoids.
In the plane, WLOG let the two points have the same ordinate. For any explicit curve, the length is given by
$$\int_{x=x_0}^{x_1}\sqrt{1+y'^2(x)}\,dx\ge\int_{x=x_0}^{x_1}dx.$$
Equality is achieved with $y'(x)=0$, i.e. $y(x)=\text{Cst}=y_0=y_1$, which is an horizontal line. The length is $x_1-x_0$.
Similary, in spherical coordinates, WLOG let one point be the pole and the other such that $\theta=0$.
Then for any trajectory $\theta=\theta(\phi)$, $$S=\int_{(\theta,\phi)=(0,\phi_0)}^{(0,\pi)}ds=\int_{\phi=\phi_0}^{\pi}\sqrt{d\phi^2+\sin^2(\phi)\,d\theta^2}=\int_{\phi=\phi_0}^\pi\sqrt{1+\sin^2(\phi)\,\theta'^2(\phi)}\,d\phi\ge\int_{\phi=\phi_0}^\pi d\phi.$$
The lower bound is achieved when $\theta'(\phi)=0$, i.e. $\theta(\phi)=\text{Cst}=0$, which is a meridian. The length is $\pi-\phi_0$.
Imagine you are at the exact centre of the sphere. You look towards the path made by connecting A and B. From your perspective it is a straight line. We know that we can't make the line shorter by passing it through the sphere since that is not allowed. If it "rises" above the surface of the sphere it will get longer and if it stays on the surface of the sphere but deviates from the straight line you can see it will increase in length as well since a line is the shortest path between two points in regular space.
Every great circle will appear to be a straight line from your point of view. Any other smaller circles that lie entirely on the surface of the sphere will appear to be circles from you point of view. Conversely, any line which appears to be straight must be an arc of a great circle, i.e. you can find a great circle which overlaps any such line. So the shortest path must exist only on a great circle.
Every great circle exactly divides a sphere into two identical semi-spheres (cuts it in half through its exact centre). It is intuitive to see that a plane intersecting a sphere through its exact centre will intersect its boundary along a great circle. The angle can be whatever you want, as long as it still passes through the centre of the sphere. If your eye is at the centre of the sphere it must also lie on the same plane, therefore everything you see on the plane will appear to be a straight line. You can only see curves as curves if your eye is above or below (or to the side, etc.) of the plane, i.e. not lying on the plane. Since every great circle lies on some plane intersecting the centre of the sphere, if your eye is at the exact centre, every great circle or arc of a great circle will appear to be straight. Any two points A and B on the surface of a sphere can be used to find a unique great circle that passes through them.
My answer is inspired in @CJ Dennis insight.
We know that the length of the segment is the same no matter how we rotate the sphere. By saying that we are at the center of the sphere looking above at the segment, we are saying that we can position the first point $A$ at the north pole, and the second point $B$ toward the east. The segment can only move in three dimensions, but since it is attached to the sphere, we have only two dimensions of free motion. As we scan the segment from north to east (from $A$ to $B$). The two free dimensions are "west-to-east", "north-to-south". If the segment $AB$ is not along a great circle, there is a projection of it into the north-to-south direction, this projection is a wiggle in the path that only will make it longer. That is, if the trajectory is in a great circle, the path looks like a straight line. There is no projection in the "north-to-south" directions and there is no shortest path than this.
Let a plane passing through the 2 points and the sphere center cut it. The shortest path is such a line of intersection. Hallmark: Surface unit normal and unit normal to the arc coincide even if there is no sphere around ... they are the same great circles..aka.. geodesics.
Given two points, think of all the segments that joint the two points. The straightest one should be the shortest. By "straightest" I mean the less curved. Curvature add length, that should be clear.
Now, take any plane intersecting the two points. Why plane? because it has the least curvature of all surfaces (0 curvature).
Then if the plane is very shallow the curvature will be larger. Hence the plane that, after intersecting both points, has the least curvature needs to be a plane that goes through the center. That is the arc of least curvature on the sphere. Then the shortest path is along a great circle.
The figure should help to explain the idea.
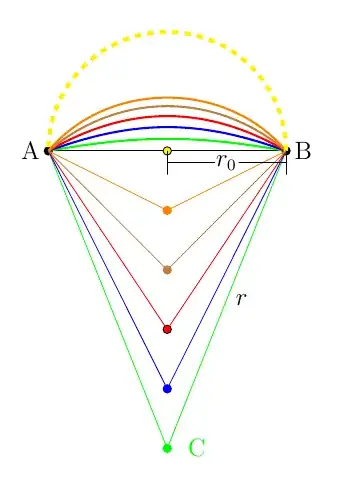
Assume that the points $A$ and $B$ are in the sides of the sphere just in front of your eyes. The center of the sphere is the green point $C$. This center is in the plane through the points $A$, $B$, and $C$ which has a great circle when intersecting with the sphere and it is the plane you are looking at (plane having the "flat" screen of your computer) As the planes with the line $AB$ on them move away from the center (up in the figure) the radius of curvature decreases (from $r$ which is the radius of the sphere down to $r_0= AB/2$ which is the radius of the intersection of a horizontal plane having the points $A$ and $B$.). See that the planes are being tilted because they are pinned to the line $AB$, so they are rotating down beyond $AB$, up toward the reader. That is, the arcs of circle that you see are all in different planes but drawn in the vertical plane. The green arc is the only arc in the vertical plane. The yellow is in the horizontal plane, and all the others are tilted planes between vertical and horizontal. The color of the dot (center) matches the color of the curve. When the plane, which started vertical rotated around the axis $AB$ until it becomes horizontal, the intersection is a the yellow dashed circle (only half shown here) in the figure. That is, the largest it can get, being flat (no wiggling. Of course you can wind all you want and that is where there is no upper limit, but the longest of the shortest is half circle with radius $r_0=AB/2$, that is $r_0 \pi/2$).
It should be clear from this figure that the green path is the shortest (after the black which is a sphere of infinite radius and has the center down at infinity).
However I decided to include a 3D picture, which I believe explains better the problem. I am using the argument on this stack exchange post: arc between two tips of vectors to plot the figure. Each arc has 200 points, and as the center move up from the origin the points get more and more spread, indicating that the length of the segments increase.
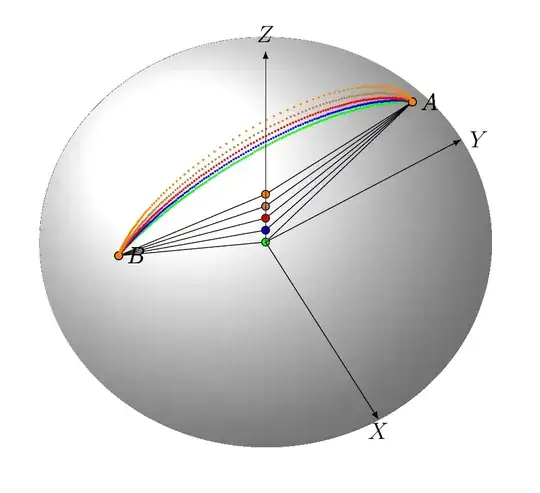
The only curve along the sphere is the green curve. All others are above, because they were rotated from the tilted plane to put them all in the same vertical plane for easier comparison.
The TiKz code for this is in this stack exchange post: draw an arc from point A to point B
It's not perfect but a more rigorous version of the following should work:
Take a sphere centered at the origin and two points. Your problem space is symmetric about the origin. Your looking for the third point on the path to define a plane that will contain the shortest path between the 2 points (and hence point c cannot be point a or b or we wouldn't have a clearly defined plane). Your three points will be co-planar. Every plane cut of a sphere results in a circle. Increasing the radius of that circle reduces the distance of the three points (triangle inequality). So we're going to change the goal of our third point that defines our plane: maximize the radius of the circle between the 2 points. Maximize radius by placing third point at center (that's the cut that's going to result in the largest circle). The 2 points will define arcs of the shortest and longest path between them, just figure out which is which.
a movie a thousand images, and an equation a thousand movies..... :)
Stare at the figure and try to draw a path shorter than that between $A$ and $B$, or $B$ and $C$, or any of the fourth vertices with any of the other three. As you said, you want a geometrical argument. It should not take time to convince you that the paths drawn on this figure (and the paths you can draw in your mind for the diagonals $A-C$ and $B-D$) are all connected to an arc that is centered at the origin. Those are parts of big circles.
columbus : a path is the graph of a function $[0,1] \to \mathbb R^{n}$ – krirkrirk Mar 08 '15 at 20:19