tl; dr: Terminology such as line gives us a convenient handle for concepts. In particular contexts, such as Euclidean geometry and spherical geometry, using line in a context-dependent way is usually more convenient than speaking of Euclidean line and spherical line for example.
Naturally, a reader has to be aware of context, the way a programmer is aware of the scope of local variables. On the other hand, most human interaction has the same technical ambiguity. When we're in the living room and we speak of "moving the chair," a listener would not naturally assume we mean "one of the chairs in the dining room, but which?"
That said, older readers may recall an Ask Marilyn column of late 1993 that hinged on the distinction between Euclidean lines and hyperbolic lines. There, because the geometries were discussed comparatively, and with each geometry providing a model of the other, "global" terminology was in order.
Arguably the question comes down to the role of definitions in mathematics. Here we have the issues of distinguishing
- Line and straight line,
- Parallel lines,
- Plane and curved plane,
- and implicitly geometry in the sense of a mathematical structure.
As noted in 5xum's answer and Somos's comment, these terms are not universal in geometry, but context-dependent. Particularly, line is used to connote a particular type of figure in Euclidean plane geometry. Even in plane geometry, however, authors will sometimes use line to connote a line segment, or to connote what others call a curved line, which civilians might call a "curve" and which mathematicians (justifiably) get all fussy over.
The term line is also sometimes used in other types of geometry to signify a geodesic, a curve with a locally length-minimizing property that can be "extended infinitely far in both directions." Calling a great circle a line in spherical geometry, or speaking of certain circular arcs in the Poincaré disk model of hyperbolic geometry, are examples. Often these geometries generalize Euclidean plane geometry, in the sense that a geometry is defined to be a set together with distinguished subsets, and geometric quantities that generalize length and/or area and/or angle, and Euclidean geometry is a particular case of the general structure.
Unfortunately for "seekers of ultimate generality," there is not a single greatest-possible generalization, no hope of identifying The One Fundamental Context.
If you're mostly interested in plane geometries (Euclidean, spherical, and hyperbolic), Patrick Ryan's Euclidean and Non-Euclidean Geometry is a clear, friendly undergraduate-level account based in linear algebra that constructs these geometries and links their synthetic properties with the analytic constructions.
Ryan amply discusses the meaning of parallel, but it may be relevant to note:
- Two lines in Euclidean or spherical or hyperbolic plane geometry are parallel if they do not intersect.
- Two parallel lines in hyperbolic geometry do not lie at constant distance, so "constant distance" is not an ideal basis for a definition because it does not generalize to contexts where stylistically "it should."
- Two lines in Euclidean space geometry that do not intersect are rarely called parallel, but instead skew.
Finally, in the hope a picture of a latitude (black) and great circle arcs (blue) on a sphere helps:

Added in Edit
In response to good comments by OP and charlie, writing more about parallels and great circles on a sphere may be in order.
Every (non-empty, non-tangential) intersection of a plane and a sphere is a circle. The circle is great if its Euclidean radius is equal to the radius of the sphere, i.e., if the plane of intersection contains the center of the sphere, and is small otherwise.
In spherical geometry, great circles are sometimes called (straight) lines while small circles (such as geographic parallels other than the equator) are not. There are multiple ways to see why this is reasonable, i.e., why parallels other than the equator are "not straight."
First, robjohn's answer here gives an analytic argument (calculus of variations), and my answer here gives a geometric argument relying on uniqueness of a shortest path between two distinct, non-antipodal points.
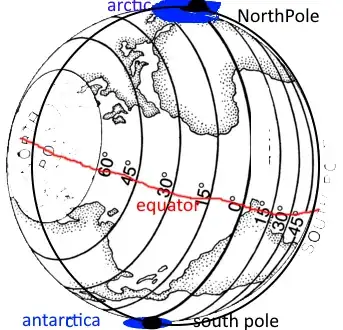
More qualitatively, the diagram above depicts the Tropic of Cancer and three great circle arcs, to illustrate visually that great circle arcs are "straighter" and therefore shorter than non-great circle arcs. The "savings" in length becomes more apparent the longer the arc, but may be difficult to see in all three cases. Here are some additional comments that may clarify:
- Imagine stretching a rubber band around a large, frictonless sphere. The band attempts to pull itself shorter, and to first order stays on the sphere. If the band lies on an equator, it rests in (unstable) equilibrium because any local perturbation makes the band longer. If the band lies on a small circle, it shrinks and pulls free because some local perturbations decrease the length. If instead we tack down the band at two points, it shrinks until the arc of band between the tacks is a piece of great circle. The original diagram may also be viewed as depicting three instances of this, with tacks placed at the dots along the parallel.
- If a non-equatorial parallel (the light blue circles in the left-hand diagram below) were a straight line, then even a Very Small parallel would be a straight line. But, for example, the parallel at latitude $89.99999^{\circ}$ is a circle $\approx 1.1$ meters in radius, visibly not "straight." Even the highest-latitude parallel in the diagram, $87^{\circ}$ (over $200$ miles in diameter), is visibly not the shortest path between its point on the prime meridian and its point on the date line (the dots at the top).
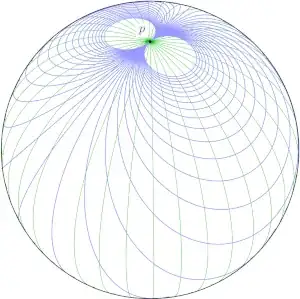
- To emphasize a possibly-underappreciated aspect of the preceding item, at each point of the earth except the poles, there passes exactly one longitude and exactly one latitude. This is an artifact of astronomy and geography: The poles are distinguished by the earth's rotation. As a geometric object, however, a sphere has Many More great circles and small circles than meridians and parallels, infinitely many through each point. In detail, if $p$ is a point on a sphere, every plane through $p$ except the tangent plane to the sphere cuts the sphere in a circle. Consequently, through every point of a sphere there is a one-parameter family of great circles parametrized by "longitude" with $p$ viewed as a pole (the green curves in the right-hand diagram below), and a two-parameter family of small circles. (The blue circles are a one-parameter family "at fixed longitude"; others are obtained by revolving about the axis through $p$.) Further, for each pair of distinct, non-antipodal points $p$ and $q$ on a sphere, there is a one-parameter family of circles through both $p$ and $q$, obtained by intersecting the sphere with an arbitrary plane containing the Euclidean line $\overline{pq}$. If we believe there is a unique shortest path/"straight line" on the sphere between $p$ and $q$, then something must distinguish it among the infinitely many circles on the sphere and passing through both points. That something turns out to be "being the short arc of great circle."