find arc between two tips of vectors in 3D

Question

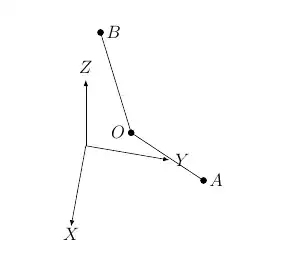
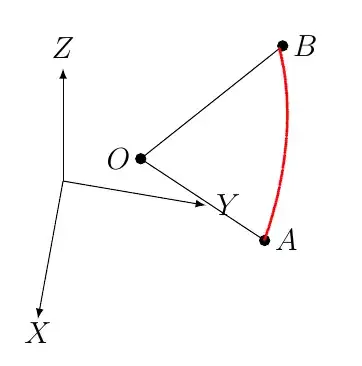
The figure helps explaining the question:

I want to use TiKz to draw an arc between $A$ and $B$. Please note several things.

1. This is a true 3D problem. There are already questions asked and solved for the 2D case. We assume that $\|B-O\|=\|A-O\|$.
2. The common point between the two vectors $O$ does not have to be the origin, but it is not a big deal to translate the whole thing.
3. I do not want 3D rotation matrices. I know the exact three coordinates of each of the three points $O$, $A$, and $B$. It is easy to compute the angle between the two vectors using dot product. So we have the range of angles. I want an equation wich is parametrized as a function of an angle between 0 and the angle between the two vectors.
4. Any point in the plane of the two vectors can be written as: $P = O + s(B-O) + t(A-O)$. I would like simple expressions for $s$ and $t$ in terms of the components of the vectors.
5. A point $X$ in the arc satisfies the equation $\|X-O\|=\|B-O\|$, $X=O + s(B-O)+t(A-O)$. 4 equations with 5 unknowns. I am missing an equation here. Actualy no. We need to eliminate 4 variables to come to the parametrization of the curve.
6. Is there an easy way to solve this? (by easy I mean no 3D rotation matrices, no large system of equations.
7. Still I would like a solution even if it is messy. Thanks.

Answer 1

The slerp formula is coordinate-free and gives you a constant-speed parametrization of the arc. In your case, assuming $O$ is at the origin, the formula is $$X = \frac{\sin\bigl((1-t)\phi\bigr)}{\sin\phi}A + \frac{\sin(t\phi)}{\sin\phi}B,$$ where $0\le t\le1$ and $\phi$ is the angle between $A$ and $B$. Observe that when $\phi=\pi/2$, the formula reduces to the usual $A\cos\theta+B\sin\theta$ parametrization of a circle, with $\theta=t\phi$.

Answer 2

Here is a direct solution.

We assume first that $O=(0,0,0)$ and then shift the origin at the end. Since $O$ is the origin the points $A$ and $B$ are true vectors, so the segment that joins them is $S= A + s(B-A)$, with $s \in [0, 1]$. When $s=0$ we are sitting on $A$ and when $s=1$ we are sitting in $B$.

The idea is to bend the segment $S$. That is, at any point $P=A + s(B-A)$ in the segment we need to shift the point by the right amount away from $O$. Call $r=\| A \| = \| B \|$. Then find the unit vector in the direction of $P$. That is \begin{equation} \bf{u} = \it \frac{P}{\| P \|} \end{equation}

which is known for each $s \in [0,1]$. Note that $\| P \| \le r$ and the equality is only achieved at the end points $A$ and $B$, and the greatest difference is in the middle where the pull up is maximum. Then multiply the unit vector by $r$ So the solution is \begin{equation} x = O + r \ {\bf{u}} \quad , \quad s \in [0, 1] \end{equation} where now $O=(o_x, o_y, o_z)$ could be a point different from 0 and $\bf{u}$ is computed after subtracting the origin from $A$, and $B$.

The figure below shows the computed arc following the algorithm above.

I find low precision at the $B$ end. This might be a deficiency on my TiKz code.

In the TeX site for StackExchange

function to find arc between two points with a center of curvature

I show the TiKz/pgfplots code for the implementation of the algorithm.

Answer 3

Let $X$ and $W$ be unit vectors in the directions of $A - O$, and $B - O$ respectively. Then let $Z$ be the unit vector in the direction of $X \times W$, and let $Y = W \times X$. We now have an orthonormal set of vectors $X, Y, Z$. If $r$ is the radius of the circle, then the curve can be parameterized $$ P(\theta) = O + (r\cos\theta)X + (r\sin\theta)Y $$ You should use values of $\theta$ between zero and $\phi$, where $\phi$ is the angle between $OA$ and $OB$.

For a more symmetrical approach, let $X$ be the unit vector in the direction that bisects $A-O$ and $B-O$, and let $Y$ be the unit vector in the direction of the chord $B-A$. Then, again, the curve can be parameterized $$ P(\theta) = O + (r\cos\theta)X + (r\sin\theta)Y $$ but the relevant values of $\theta$ are now those in the range $-\tfrac12\phi \le \theta \le \tfrac12\phi$.