Where is my error when setting up the differential equation to find the length of a path on a sphere

Question

I have a sphere and I want to find the equation of the curves which give us the shortest path between two points laying on its surface.

By using the Euler-Lagrange equation, I need to find the value of the Lagrangian function $F$, therefore we want find a proper expression for $dS$: a very small portion of the curve on the sphere.

The problem

The typical setting of finding a solution via the Euler-Lagrange equation is to achieve the following:

$$ dS = F(x,y,y^\prime)dx \implies S = \int_{x_1}^{x_2} F(x,y,y^\prime)dx $$

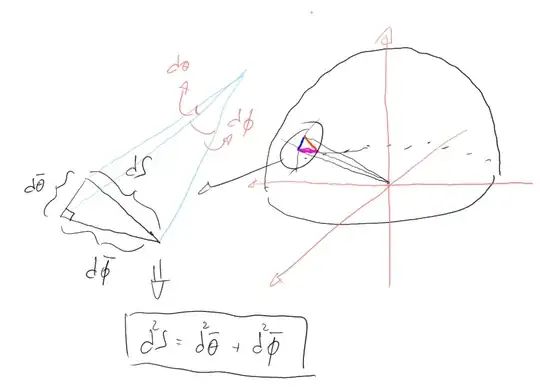
So I start from $dS$, and try to find a relation which, on a sphere, involves the two angles $\phi$ and $\theta$ in the polar coordinates (sphere centered at the origin of the axes: $\phi$ is the angle on the XY plane, $\theta$ the vertical angle).

As you can see from the picture, on the spherical surface, my $dS$ is basically a line. So I decompose that vector in two components that are perpendicular. I obtain a very small right triangle laying on the plan which is tangent the sphere and contains $dS$:

$$ (dS)^2 = (d\bar{\phi})^2 + (d\bar{\theta})^2 = r^2 (d\phi)^2 + r^2(d\theta)^2 $$

Considering $d\bar{\phi}$ and $d\bar{\theta}$ to be the very small arcs subtended by their respective angles (two of the 3 polar coordinates). These two quantities can also be approximated to lines.

My approach is wrong, why?

However, the equation I managed to get at is wrong. This problem is very classic and its solution is different. So my question is: where is my mistake?

Important I know that the shortest path between two points on a sphere is the arch connecting them. This is not the point of this question. In this question, I want to know what my mistake is in deriving the differential equation to calculate function $y(x)$.

Answer 1

If you have a short curve (on the unit sphere) along which $\Delta \phi = 0.1$ and $\Delta \theta = 0$, how long is it (either in Euclidean space or along the sphere surface)? Answer: roughly $\Delta \phi$. So the $d\phi^2$ portion of your formula is good. [It's not clear from your picture, but I'm using $\phi$ for latitude (with $\phi = 0$ at the north pole) and $\theta$ for longitude. ]

What if you have a short curve for which $\Delta \theta = 0.1$ and $\Delta \phi = 0$? How long is it? Well, if $\phi = \frac{\pi}{2}$, then it's about $\Delta \theta$ long. But if $\phi \approx 0$, then it's basically zero-length. So the $d\theta$ term in your formula needs a factor of $\sin \phi$: $$ ds^2 = d\phi^2 + \sin^2 \phi ~~d\theta^2. $$