Prove that the shortest path between two points on the unit sphere is an arc of a great circle connecting them
Great Circle: the equator or any circle obtained from the equator by rotating further: latitude lines are not the great circle except the equator
I need help with starting this question, because I am not quite sure how to prove this.
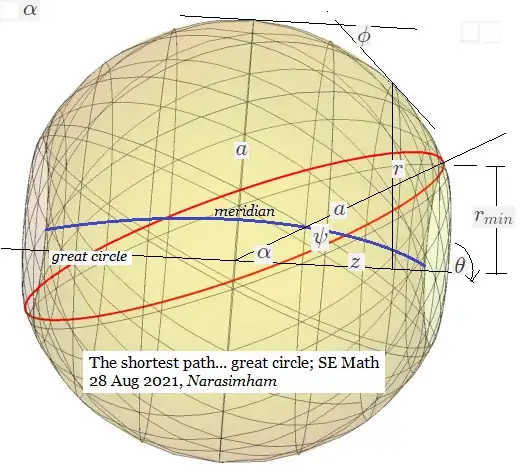
Calculus of Variations
Using latitude, $\phi$ and longitude, $\theta$, we have $$ 1=\cos^2(\phi)\left(\frac{\mathrm{d}\theta}{\mathrm{d}s}\right)^2+\left(\frac{\mathrm{d}\phi}{\mathrm{d}s}\right)^2\tag1 $$ Integrating $(1)$ with respect to $s$, taking the first variation, and integrating by parts, we get $$ \scriptsize\delta s=\int\left[\left(\color{#C00}{2\sin(\phi)\cos(\phi)\,\frac{\mathrm{d}\theta}{\mathrm{d}s}\,\frac{\mathrm{d}\phi}{\mathrm{d}s}-\cos^2(\phi)\,\frac{\mathrm{d}^2\theta}{\mathrm{d}s^2}}\right)\delta\theta-\left(\color{#090}{\sin(\phi)\cos(\phi)\,\left(\frac{\mathrm{d}\theta}{\mathrm{d}s}\right)^2+\frac{\mathrm{d}^2\phi}{\mathrm{d}s^2}}\right)\delta\phi\right]\mathrm{d}s\tag2 $$ Orthogonality requires that a curve where we have $\delta s=0$ for any $\delta\theta$ and $\delta\phi$ must satisfy $$ \color{#C00}{\frac{\mathrm{d}^2\theta}{\mathrm{d}s^2}=2\tan(\phi)\,\frac{\mathrm{d}\theta}{\mathrm{d}s}\,\frac{\mathrm{d}\phi}{\mathrm{d}s}}\tag3 $$ and $$ \color{#090}{\frac{\mathrm{d}^2\phi}{\mathrm{d}s^2}=-\sin(\phi)\cos(\phi)\,\left(\frac{\mathrm{d}\theta}{\mathrm{d}s}\right)^2}\tag4 $$
Solving the Equations
$$
\begin{align}
\log\left(\frac{\mathrm{d}\theta}{\mathrm{d}s}\right)
&=2\log(\sec(\phi))+\log(\cos(\epsilon))\tag{5a}\\
\frac{\mathrm{d}\theta}{\mathrm{d}s}
&=\cos(\epsilon)\sec^2(\phi)\tag{5b}\\
\left(\frac{\mathrm{d}\phi}{\mathrm{d}s}\right)^2
&=1-\cos^2(\epsilon)\sec^2(\phi)\tag{5c}\\
s
&=\int\frac{\mathrm{d}\phi}{\sqrt{1-\cos^2(\epsilon)\sec^2(\phi)}}\tag{5d}\\
&=\int\frac{\mathrm{d}\sin(\phi)}{\sqrt{\cos^2(\phi)-\cos^2(\epsilon)}}\tag{5e}\\
&=\int\frac{\mathrm{d}\sin(\phi)}{\sqrt{\sin^2(\epsilon)-\sin^2(\phi)}}\tag{5f}\\
&=\sin^{-1}\left(\frac{\sin(\phi)}{\sin(\epsilon)}\right)+s_0\tag{5g}\\[9pt]
\end{align}
$$
Explanation:
$\text{(5a)}$: divide $(3)$ by $\frac{\mathrm{d}\theta}{\mathrm{d}s}$ and integrate
$\text{(5b)}$: remove the log
$\text{(5c)}$: apply $(1)$ to $\text{(5b)}$
$\text{(5d)}$: separate the differential equation and integrate
$\text{(5e)}$: multiply the integrand by $\frac{\cos(\phi)}{\cos(\phi)}$
$\text{(5f)}$: $\cos^2(x)=1-\sin^2(x)$
$\text{(5g)}$: evaluate the integral
Solving $\text{(5g)}$ for $\sin(\phi)$ gives
$$
\bbox[5px,border:2px solid #C0A000]{\sin(\phi)=\sin(s-s_0)\sin(\epsilon)}\tag6
$$
Furthermore,
$$
\begin{align}
\theta
&=\int\frac{\cos(\epsilon)\,\mathrm{d}(s-s_0)}{1-\sin^2(s-s_0)\sin^2(\epsilon)}\tag{7a}\\
&=\int\frac{\cos(\epsilon)\,\mathrm{d}\tan(s-s_0)}{\sec^2(s-s_0)-\tan^2(s-s_0)\sin^2(\epsilon)}\tag{7b}\\
&=\int\frac{\cos(\epsilon)\,\mathrm{d}\tan(s-s_0)}{1+\tan^2(s-s_0)\cos^2(\epsilon)}\tag{7c}\\[6pt]
&=\tan^{-1}(\tan(s-s_0)\cos(\epsilon))+\theta_0\tag{7d}
\end{align}
$$
Explanation:
$\text{(7a)}$: apply $\text{(5h)}$ to $\text{(5b)}$, separate the differential equation, and integrate
$\text{(7b)}$: multiply the integrand by $\frac{\sec^2(s-s_0)}{\sec^2(s-s_0)}$
$\text{(7c)}$: $\sec^2(x)=1+\tan^2(x)$
$\text{(7d)}$: evaluate the integral
Solving $\text{(7d)}$ for $\tan(\theta-\theta_0)$ gives $$ \bbox[5px,border:2px solid #C0A000]{\tan(\theta-\theta_0)=\tan(s-s_0)\cos(\epsilon)}\tag8 $$
Compare with a Great Circle
Given the parameterization in $\mathbb{R}^3$ of a great circle $$ (x,y,z)=(\cos(s-s_0),\sin(s-s_0)\cos(\epsilon),\sin(s-s_0)\sin(\epsilon))\tag9 $$ we get $$ \sin(\phi)=z=\sin(s-s_0)\sin(\epsilon)\tag{10} $$ and $$ \tan(\theta-\theta_0)=\frac yx=\tan(s-s_0)\cos(\epsilon)\tag{11} $$ Equation $(10)$ matches equation $(6)$ and equation $(11)$ matches equation $(8)$. Thus, the shortest path between two points on a sphere is an arc of a great circle.
Plotting the Solved Equations
Since $\phi\in\left[-\frac\pi2,\frac\pi2\right]$, we can get $\phi$ by applying $\sin^{-1}$ to $(6)$:
$$
\bbox[5px,border:2px solid #C0A000]{\phi=\sin^{-1}(\sin(\epsilon)\sin(s-s_0))}\tag{12}
$$
However, to get $\theta-\theta_0$, we cannot simply apply $\tan^{-1}$ to $(8)$. Instead, we note that
$$
\begin{align}
\tan((\theta-\theta_0)-(s-s_0))
&=\frac{\tan(\theta-\theta_0)-\tan(s-s_0)}{1+\tan(\theta-\theta_0)\tan(s-s_0)}\tag{13a}\\
&=\frac{\tan(s-s_0)(\cos(\epsilon)-1)}{1+\cos(\epsilon)\tan^2(s-s_0)}\tag{13b}
\end{align}
$$
Explanation:
$\text{(13a)}$: formula for the tangent of a difference
$\text{(13b)}$: apply $(8)$
Thus, we get
$$
\bbox[5px,border:2px solid #C0A000]{\theta-\theta_0=(s-s_0)-\tan^{-1}\left(\frac{(1-\cos(\epsilon))\tan(s-s_0)}{1+\cos(\epsilon)\tan^2(s-s_0)}\right)}\tag{14}
$$
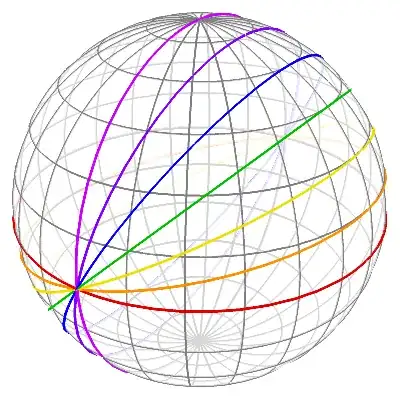
Great circles with $\epsilon=\left\{\color{#DF0000}{0^{\large\circ}},\color{#FF8F00}{15^{\large\circ}},\color{#EFDF00}{30^{\large\circ}},\color{#00BF00}{45^{\large\circ}},\color{#0000FF}{60^{\large\circ}},\color{#8000FF}{75^{\large\circ}},\color{#CC00FF}{90^{\large\circ}}\right\}$ plotted using $(12)$ and $(14)$.
Two approaches are outlined in the following:
The great circle is an intersection between the sphere and plane. It is a geodesic, a displaced equator with vanishing geodesic curvature. It contains the sphere center. When it does not contain the sphere center it is a small circle... having non-zero geodesic curvature $k_g.$
Many small circles go through two points A and B of polar angles $ \theta_{1,2}$ and among them the shortest distance geodesic line runs. It is characterized by the Clairaut's Law derived in text books of differential geometry with Liouville thm/ formula for geodesic curvature $ k_g=0$, briefly outlined here using standard notation of the second and first fundamental forms of surface theory:
$$k_g= \psi' + P u'+ Q v';\; P * 2HE= 2 EF_1-FE_1-EE_2;\;Q* 2HE= EG_1-FE_2; \;$$
Where subscripts $1,2 $ are for meridian and circumferential directions.
The same can be also established by arc length (here independent variable s=arc used for priming ) minimization in Variational calculus using cylindrical coordinates $ ( r, \theta, z )$.
$$ds =\sqrt{ (r d \theta)^2 + dr^2+ dz^2 }= \sqrt{ r ^2 + r{'^2}+ z{'^2}}d \theta$$
Using Euler-Lagrange theorem of two dependent variables $ r,\theta $ from $ (r,\theta,z)$
$$\sqrt{ r ^2 + r{'^2}+ z{'^2}}-r'\cdot \frac{r'}{\sqrt{ r ^2 + r{'^2}+ z{'^2}}}-z'\cdot \frac{z'}{\sqrt{ r ^2 + r{'^2}+ z{'^2}}}= const $$
$$ \frac{r^2}{\sqrt{ r ^2 + r{'^2}+ z{'^2}}}= r\cdot \sin \psi = const = r_{min}$$
where the constant $r_{min}$ is interpreted as the small circle radius which is tangential to all red great circles obtained by rotation ofall great circles with respect to the axis of symmetry $ r=0 $ shown.
Projections of great circles on $ (x/y, y/z, z/x) $ planes are all ellipses with inclination $\alpha = \sin ^{-1}\dfrac{r_{min}}{a} $
The following relations hold $ \phi= slope, \psi = $ angle the great circle makes to meridian.
$$ \cos\phi= \frac{r}{a},\;\sin \psi \cos \phi= \frac{r_{min}}{a}$$
HINT: (Edited 8/27/2021) Start with two points on the equator. Every great circle (except one) meets the shorter great circle arc joining them in at most one point. Let $\Sigma$ be the set of great circles meeting it in one point. Show that for any other curve $C$ joining the points, there must be an open set containing $\Sigma$ of great circles meeting $C$ in at least two points.
