Is there a word for a polyomino with $n$ connected cells in each row?

Question

Here are some examples for $n = 4$.

Answer 1

There does not seem to be a standard term, but in their paper The gap number of the T-tetromino the author use the term cylinder. In their paper they use it as tool to find the minimum number of monominoes necessary to tile rectangles by T-tetrominoes and monominoes.

Two other places where cylinders arise:

To determine if a figure is tileable by dominoes, we can remove a cylinder with even width and bring the two pieces together (without moving either piece vertically); the original figure is tileable by dominoes if and only if the new figure is tileable by dominoes. (There are a few technicalities that I omit here to make it completely true). This makes it very simple to answer domino tiling problems by inspection.

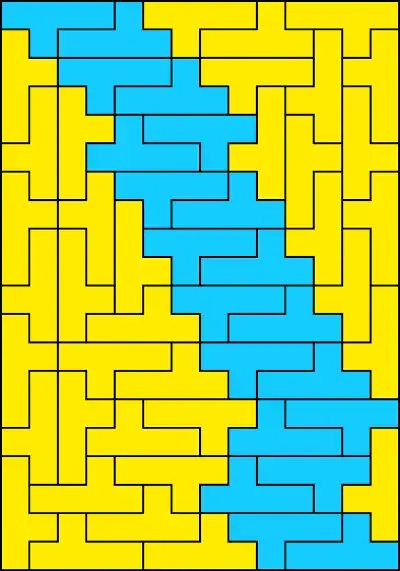
To prove which rectangles have fault-free tilings, a typical technique is to give fault-free tilings of a few basic rectangles, and then to show how these can be extended to other rectangles by inserting cylinders. For example, in the figure below, the blue cylinder can be repeated any number of times (including 0) to give various fault-free tilings by the Y-pentomino.