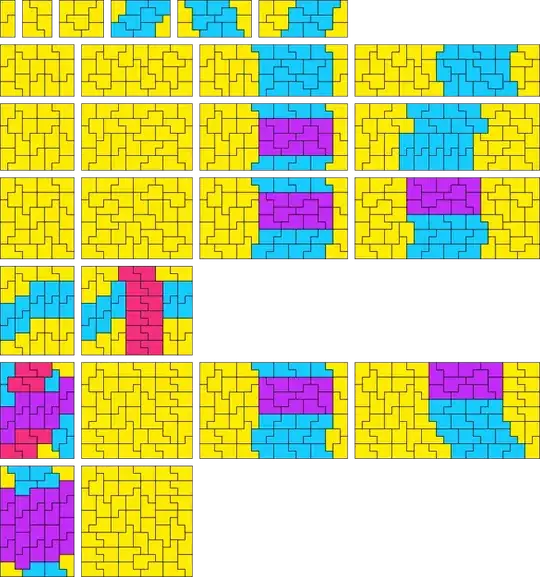
I am trying to find all rectangles with fault-free tilings of the P pentomino. (A fault is a vertical or horizontal line inside the rectangle that is not crossed by any tiles; a fault-free tiling is thus a tiling without such lines.)
My basic strategy is to find "basic" fault free tilings, and then extend them.
So far, the following extensions are possible:
- $5 \times 2n$ rectangles can be extended to $5 \times (2n + 6k)$ for $n \geq 1$.
- $m \times 2n$ rectangles can be extended to $(m + 5) \times 2n$ for $m \geq 5$ and $n \geq 2$.
- $(5m + 5) \times (2n + 5)$ rectangles can be extended to $(5m + 15) \times (2n + 5)$ for $m, n \geq 1$.
And I have the following basic rectangles:
- $2 \times 5$, $4 \times 5$, $6 \times 5$
- $7 \times 10$, $9 \times 10$, $11 \times 10$
- $7 \times 15$, $9 \times 15$, $11 \times 15$, $13 \times 15$, $15 \times 15$
The idea is to find if all possible rectangles can have fault free tilings, so I use this table for comparison.
My question is, is there some systematic way to deal with this "system of rectangles"? How do I know I have everyone? Or if I can make either list of basic rectangles or the list of extensions shorter?
(The P-pentomino is probably manageable with a bit of care, but I make many mistakes which made me wonder if there is a more systematic way. Also, I plan to examine the Y-pentomino next, and since it has 40 prime rectangles, I expect it to have at least as many basic rectangles.)
This picture summarizes the above. Tilings that only have yellow tiles are "basic"; colored tiles are "cylinders" inserted into basic tilings to extend them.