8

As far as I know, it is an open problem whether there exists a single connected tile that tiles the plane only non-periodically.

Is the situation different for a strip? (Or, for that matter, a half strip, or quadrant, or bent strip.) I mean, is it possible for a single tile to tile a strip only non-periodically (or half strip, quadrant, bent strip), or is it also unknown?

(I ask generally, but I am particular interested in tiles that are polyominoes.)

To give some context: I'm on a self-study adventure of polyominoes and their tilings especially (I asked some previous questions that up came up in this context: Does every domino tiling have at least two “exposed” dominoes? and What rectangles can a set of rectangles tile?). This latest one comes from trying to see which strips (and half strips etc.) a polyomino can tile. One way to do this would be to show that you cannot form any parallelogram-like* pieces that can can be joined repeatedly to form the strip (or half strips etc.) But this will only work if strips (etc.) can always be tiled periodically if at all.

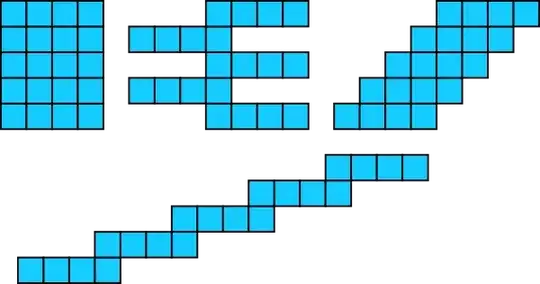
(*) Parallelogram-like piece = a piece that has four "sides"; two opposites that are straight and the same length, and the other two no necessarily straight but the onbe is a translate of the other. For polyominoes, it's figures where all rows have equal number of cells and they are all row-connected. (I also asked here if there is a term for such polyominoes: Is there a word for a polyomino with $n$ connected cells in each row?. I did not get an answer, and after looking through hundreds of papers I haven't found one.) Here are some examples.

enter image description here

(Clearly such can be put together to tile a strip.)

Herman Tulleken
  • 3,608
  • Maybe you can ask this question at https://mathoverflow.net/. This sounds more like a research-leveled question, and some experts there may know something. – Batominovski Nov 21 '17 at 01:17
  • OK thanks for the advice; I will let it stand here for a few days and then try there (it's always very hard to know if questions are within their scope because I am not an expert in these topics.) – Herman Tulleken Nov 21 '17 at 01:21
  • 3
    You may want to look at https://lipn.univ-paris13.fr/GDR-IM-2016/SLIDES/jeandel.pdf – it's concerned with tiling the plane, but approaches that problem via tiling strips, so it may have something useful for you. – Gerry Myerson Nov 21 '17 at 01:40
  • 3
    Nishant Chandgotia, A tiling problem, available at http://www.math.tau.ac.il/~nishant/Research_files/Notes_files/Tiling.pdf gives an argument, bottom of page 2 to top of page 3, which "shows a strip can be tiled if and only if there exists a periodic tiling." I have not tried to verify it. – Gerry Myerson Nov 21 '17 at 01:49
  • @GerryMyerson Thanks, it answers the question (at least for Wang tiles) and the way it is handled in the slides makes it quite clear. Could you put that in an answer? (Otherwise I could.) One question: If it's known for Wang tiles does it imply the same for all tilings? (Is this a quick question or should I ask another?) – Herman Tulleken Nov 22 '17 at 10:42
  • I'm quite happy for you to post an answer. I can't help with your other question – all I know about tilings is what I can find on the internet. – Gerry Myerson Nov 22 '17 at 11:52

1 Answers1

9

For Wang tiles and polyominoes: if a tile set tiles a strip, there exists a periodic tiling of the strip by the tile set.

The argument that follows is roughly from the link provided by Gerry Meyerson: https://lipn.univ-paris13.fr/GDR-IM-2016/SLIDES/jeandel.pdf

Although they don't deal with this issue specifically it's implicit in how their algorithm works.

I'm going to make the argument for polyominoes, but it should be clear that it works for Wang tiles and a whole variety of other tilesets too.

For any strip tiling, we can cut up the tiling into new vertical tiles as shown in this image:

enter image description here

Here, the original tile set is L-tetrominoes, and the new vertical tiles are the strips outlined in black.

This will give us a new tile set $T_1, \cdots, T_k$, which is finite. We have to take care that tiles that cut polyominoes in different parts are distinct. For example, even though the four tiles shown here look the same, they should be different.

enter image description here

This allows us to make a directed graph with the new tiles as vertices, and an edge from $T_i$ to $T_j$ if placing $T_j$ to the right is a legal configuration considering the original tiles. For example, in the figure above, if we label the tiles $T_1, \cdots, T_4$, then we have $T_1 \rightarrow T_2 \rightarrow T_3 \rightarrow T_4 \rightarrow T_1$, but not for instance $T_1 \rightarrow T_3$, since this "leaves out a piece from certain tiles of the original set".

For a strip tiling to exist, it must be possible to visit nodes following the edges in an infinite path. But the number of vertices is finite, therefor we must have a cycle. And any cycle means we can build a periodic tiling using the new tiles, which corresponds to a periodic tiling of the original tiles too.

Herman Tulleken
  • 3,608