What is the most fuel efficient way out of the Solar System?

Question

I understand with current technology we can't just fly a straight line out of the solar system but which way out would need the least fuel?

Currently to navigate the solar system it is a dance around the planets using sling shots, gravity assist and such.

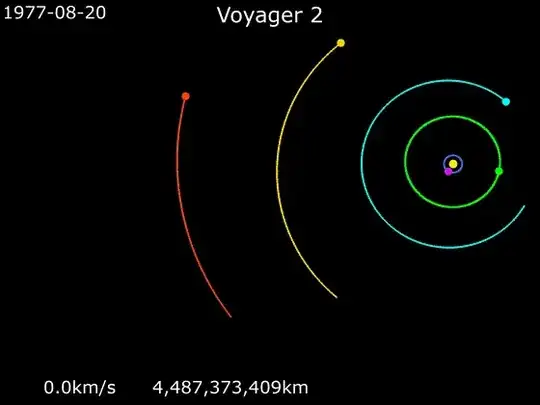
The Ground Tour trajectory of Voyager 2 "used" the first three of the four large planets Jupiter, Saturn, Uranus, and Neptune, but this was optimized for time, and it ended up with far more than heliocentric escape velocity.

Suppose instead the goal of the exercise were to barely achieve heliocentric escape velocity using the minimum fuel or delta-v, starting from LEO, with a lot more flexibility on time, say roughly 100 years from launch to achieving escape velocity (C3=0). Assume you can start at optimum configuration of the planets within their orbits.

What would that trajectory look like? Would it still use all four of these planets, or could you get by with fewer? Would it make sense to look inward, using the four rocky planets instead?

As a side question, would having even more planets present on the way out always help?

above: Voyager 2 Grand Tour. Source

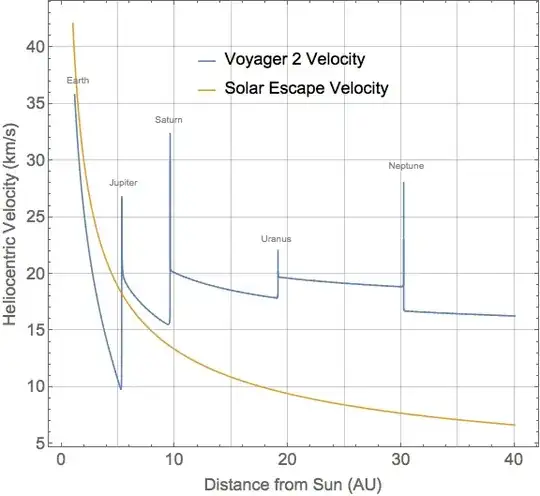
below: Voyager 2 Grand Tour Heliocentric velocity. Source

direction. "Way" implies a 'way of means' IMO. Which would use tidel influences on a machine of planetary scale. Fuel consumption: zero. — Mazura, Feb 27 '19 at 23:59
This is the second question in a few days about escaping the solar system. I'm wondering if there's something specific I need to be worried about... — Richard, Feb 28 '19 at 00:40
I still don't get what was wrong with the gif, other than it doesn't show the sun bobbing up and down in the plane of the Milky Way. — Mazura, Mar 02 '19 at 06:12
@DavidHammen I've added some wording, and some more relevant graphics; many of us can still benefit from being reminded of what actually happened kinematically in the grand tour. How does this wording look? — uhoh, Mar 04 '19 at 12:45
The most fuel efficient way out of the solar system is no fuel. Use a solar sail. — Sovereign Inquiry, Nov 29 '21 at 22:13
I believe the initial sentence of this question is incorrect. The New Horizons launch was very close to solar system escape velocity even without the Jupiter gravity assist. In fact, there were backup plans to complete the mission to Pluto without the assist if the necessary launch window could not be met. It would have been several years later, but my impression is that it still would have been an escape trajectory. — Mark Foskey, Mar 07 '23 at 03:24

Steve Linton · Accepted Answer · 2019-03-25T09:08:53.330

24

The most fuel efficient way to leave the solar system at present, is to launch into a trajectory that (like that used for Gallileo) may well involve one or several gravity assists from Earth or Venus, but which eventually gets you to Jupiter. If you can get to Jupiter you can almost certainly do so in such a way as get a slingshot into a solar escape trajectory. Encounters with other planets after that are just "icing on the cake" (you get into a faster escape trajectory) and like all gravitational slingshots there is a problem of diminishing returns. The faster you are going, the less good they do you. Anyway the problem as stated is basically the same one as getting to Jupiter.

The Trident mission proposal illustrates a trajectory of this kind. The initial launch is to a Venus transfer orbit. After that, it uses gravity assists at Venus, Earth (twice) and Jupiter to get to Neptune with no significant further fuel consumption and at a speed which will certainly take it out of the solar system.

A related question is how to get leave the solar system going as fast as possible for a given supply of fuel (equivalently a given total delta-V). You still start by going to Jupiter. Then you use the gravity of Jupiter to drop you into as energetic an orbit as possible, passing as close to the Sun as your systems can survive. Once there you burn all your remaining fuel and then you coast. You might gain a little from encounters with Jupiter and/or Saturn on the way out, but you are moving so fast it doesn't really matter.

The Thousand AU study reckoned you could achieve exit from the inner solar system at a velocity of perhaps 10-15 AU/year using this technique with a large current launcher. An additional advantage is that you can exit in any direction you like. more or less.

edited Mar 25 '19 at 09:08

answered Feb 27 '19 at 17:28

Steve Linton

19,594
1
64
94

+1 that would depend on how close Venus is to Earth. If the scale of the gif is correct and you used a straight line out what would be the fastest way out? – Muze Feb 27 '19 at 17:33
1

@Muze check out the parker solar probe's trajectory, except at the closest point of approach instead of doing science you'd do a burn. I'd love to see the actual numbers though, given a particular craft and a particular perigee. – Magic Octopus Urn Feb 27 '19 at 17:36
1

If for some reason you don't want to do any gravity well maneuvers at all then you want to launch tangentially to Earth's orbit to get maximum benefit from Earth's orbital velocity. You'd want to launch at midnight so that Earth's rotational velocity added in as well. But this is still much worse than going via a close solar encounter – Steve Linton Feb 27 '19 at 17:40
@SteveLinton I will read on this in depth thanks again. – Muze Feb 27 '19 at 17:48
3

@Muze What is the fastest way out is almost certainly not the most fuel efficient. Venus is the place we can get for the least energy and once you can reach another world you can escape by playing billiards--but that's a slow process unless everything is neatly lined up for you like with the Voyager probes. – Loren Pechtel Feb 27 '19 at 22:13
1

How about the Voyager/Grand Tour option, where your gravity assist from Jupiter is followed by ones from Saturn, Uranus, and Neptune? AFAIK, the Voyagers didn't use fuel (other than a small amount for mid-course corrections) once they had boosted from Earth orbit. Getting to Jupiter via Venus/Earth assists might make it even more fuel-efficient. – jamesqf Feb 28 '19 at 02:09
9

@Muze, If you think that the most efficient path would be a "straight line," then you are pretty far from understanding how objects move in the Solar system. Far enough that the kind of answers that you can find on a web site like this probably are going to be less than helpful. You need some book learning or some classroom learning. Good luck! – Solomon Slow Feb 28 '19 at 03:00
@jamesqf It all depends how much delta-V you have. If you get to Jupiter with enough fuel in the tank, you want to use that fuel as close to the Sun as you can, so you use Jupiter to put you on a hyperbolic orbit that grazes the Sun (very fast) use your fuel there to speed up. A gravity assist from one or more of the giant planets on the way out would be icing on the cake, but the faster you are already going the less useful that is. – Steve Linton Feb 28 '19 at 08:15
@jamesqf From Wikipedia: " The particular alignment occurs once every 175 years." – JollyJoker Feb 28 '19 at 09:14
1

@JollyJoker: True, but the OP was asking for the most efficient course, not one that could be taken immediately :-) – jamesqf Feb 28 '19 at 18:21
@Steve Linton: But is having fuel left to burn when you're close to the Sun the most fuel-efficient? I can see that it would be faster, but the Grand Tour (or even just Jupiter-Saturn) uses only fuel to boost out of Earth gravity to Jupiter. – jamesqf Feb 28 '19 at 18:24
1

@SteveLinton, actually, you want to launch sometime before midnight. Earth's gravity will bend your trajectory, and you want to wind up on a path tangent to Earth's orbit. (Exact timing depends on your thrust-to-weight ratio and final velocity.) – Mark Feb 28 '19 at 20:40
1

@jamesqf Yes, I guess if you take the question literally as asked -- how to leave the solar system (whatever that means) with least fuel, you probably wait until exactly the right moment, launch to Venus (possibly after spending some time using the Moon's gravity to raise your apogee) and then play billiards for a few decades until you can finally get a Jupiter encounter that can eject you from the Solar system. Very little fuel, but really, really slow. – Steve Linton Feb 28 '19 at 20:48
just fyi the original GIF is long gone. I've enhanced the wording of the question but I think it doesn't affect your answer. – uhoh Mar 04 '19 at 12:54

Mark · Answer 2 · 2019-03-01T03:10:43.027

11

If you want to avoid gravity assists, the most fuel-efficient way out of the Solar System is to launch due East from from a launch site in the Ecuadorean Andes, sometime before local midnight on a January 3 when there's a new moon. This gives you the maximum possible benefit from the Earth's movement, leaving only about 12,000 m/s of delta-V needed in excess of Earth escape velocity.

(Rough estimate: a Saturn V could barely put New Horizons directly into a solar escape trajectory. This is why we use gravity assists instead.)

edited Mar 01 '19 at 03:10

answered Feb 27 '19 at 21:45

Mark

15,260
60
70

This is intriguing! I've just asked Launching east from a mountain on the equator at midnight during a new moon; ranking of each contribution? – uhoh Feb 28 '19 at 02:32
Not quite work a downvote since a simple edit will fix this answer. It would be better to launch on about the third of January (Earth perihelion) than the fourth of July (Earth aphelion). The advantage from a higher orbital velocity outweighs the disadvantage from being deeper in the Sun's gravitational well thanks to the Oberth effect. – David Hammen Feb 28 '19 at 17:02
@DavidHammen, you sure about that? At aphelion, I get a solar escape velocity of 41174 m/s and an orbital velocity of 29290 m/s for a net required velocity of 11884 m/s. At perihelion, I get a solar escape velocity of 42480 m/s and an orbital velocity of 30290 m/s, for a net required velocity of 12118 m/s. The reduced escape velocity from a higher orbit slightly outweighs the loss in Earth orbital velocity. – Mark Feb 28 '19 at 20:36
2

@Mark - Quite positive. I agree with all your numbers to within a few meters per second except the escape velocity at aphelion, which is low by about 600 m/s. Moreover, look at the vis viva equation, $v^2 = \mu\left(\frac2r-\frac1a\right)$. Since escape velocity $v_e$ is ${v_e}^2 = \frac{2\mu}r$, another way to write the vis viva equation is ${v_e}^2-v^2 = \frac\mu a$. The difference between escape velocity and orbital velocity is thus $v_e-v = \frac{\mu/a}{v_e+v}$. Periapsis maximizes both $v_e$ and $v$ and therefore minimizes the difference between escape velocity and orbital velocity. – David Hammen Feb 28 '19 at 23:39
Now, how to escape Sol's gravity altogether? – AndrewMaxwellRockets Mar 01 '19 at 01:57
@DavidHammen, I re-did the math and got an aphelion escape velocity of 41774. Looks like you're correct. – Mark Mar 01 '19 at 03:10

AndrewMaxwellRockets · Answer 3 · 2019-02-28T03:21:36.773

0

Launching from the west side of Earth and taking a slingshot course by the sun for a turn of about 90*, then doing another sling past Jupiter(burning all your fuel) would, I think, be the most efficient way to do this. Ion engines and mirrors would be the most efficient propulsion method as well, however I would recommend using common LOXY engines to get into orbit, and then the ion engines to break orbit and head towards the sun. It would work, if you were to launch your rocket today, along the orbital path of the planets...

However, another way to do it(again with the help of the sun) would be to go into LEO, and then set your periapsis to the 'night side' of Earth. Then, at periapsis, have your engines at full blast until the other side of your orbit goes to the opposite side of Sol, and then coast till you reach the bottom, and, again, go full blast. by the time you are done accelerating, your apoapsis should be well out of the solar system.

There is no way to go "straight" out of the solar system without being accelerated and decelerated. Gravitational forces will always be acting upon you, and until you get to the point where the nearest extrasolar body's gravity is stronger than the sun's, you won't be "out" of the solar system.

edited Feb 28 '19 at 03:21

answered Feb 27 '19 at 17:37

AndrewMaxwellRockets

355
2
10

3

Light pressure at Earth's distance from the Sun is about $6\mu Pa$. An alumnium sail 50 nm thick (much thinner and it would be transparent) has areal density about $1.3 \times 10^{-4} kg/m^2$ so with no payload would accelerate at $4\times 10^{-2} m/s^2$ (abotut 4 milli gravities). By the time it reached the orbit of Mars (ignoring the Sun's gravity) it would be moving at something in the ballpark of $100 km/s$. So yes, a very thin solar sail with no allowance for rigging or payload could escape the solar system. – Steve Linton Feb 27 '19 at 18:26
7

@SteveLinton, the nice thing about solar sails is that both gravity and light pressure fall off as the inverse square of distance. If you've got a sail that provides acceleration at one distance from the Sun, it'll provide acceleration at all distances from the Sun. – Mark Feb 27 '19 at 23:47
@SteveLinton this is another answer. Thumbs up. – Muze Feb 28 '19 at 04:52
@Mark: Not all distances, maybe till it reaches the heliopause, I presume? – sampathsris Feb 28 '19 at 04:54
1

@sampathsris, until other stars start interfering with it. Most of the force on a solar sail comes from sunlight, not the solar wind, and that doesn't stop at the heliopause. – Mark Feb 28 '19 at 06:20
Oh yeah. Light sail. I feel dumb now. :D – sampathsris Feb 28 '19 at 06:33
@Mark. It's true that the ration of light pressure and gravity remains constant but the absolute acceleration drops off. There is a maximum speed achievable by a light-sail driven solely by sunlight starting at a given point. – Steve Linton Feb 28 '19 at 08:12
3

If I'm reading this correctly this is definitely not the most fuel efficient way to leave the solar system. Going to the sun with an impulsive maneuver straight from earth is significantly more expensive than simply going straight to an escape trajectory. From LEO, it takes ~7 km/s of delta-V to get on an escape trajectory out of the solar system. To end up on a trajectory that goes near the sun takes on the order of ~20 km/s. – Kyle Feb 28 '19 at 09:39
3

This should not be the accepted answer. As @Kyle noted, without gravity assists, it's very harder to get close to the Sun than it is to simply escape the solar system. Gravity assists change this dynamic. Steve Linton's answer is much better in this regard. – David Hammen Feb 28 '19 at 11:36
@Kyle I'm talking about LEAVING the solar system altogether, to leave Sun orbit, to break away from the gravity of all our solar system's bodies. – AndrewMaxwellRockets Feb 28 '19 at 23:08
@AndrewMaxwellRockets So am I (just getting to Earth escape would be a paltry 4 km/s). To get near the sun you have to get rid of nearly all of Earth's orbital velocity, which is near 30 km/s (the 20 km/s figure is because I figured in a LEO departure and the Oberth effect near Earth helps out). To get on an escape trajectory out of the solar system you only need about 41% of that (the 7 km/s figure is for the same departure as above). – Kyle Mar 01 '19 at 05:20
You have 3 up votes and 3 down votes as you earn more rep you will see more. – Muze Mar 04 '19 at 17:22

score 0 · Answer 4 · answered Mar 07 '23 at 01:32

Check out Could a “solar gravitational synchrotron ” use solar thermal rockets to "powerslide" spacecraft out of the solar system?

This strategy uses a solar thermal rocket and ISRU water to accelerate spacecraft to solar escape velocity. There are no timing limitations from gravity assist rendezvous. Any departure direction in the ecliptic is allowed.

What is the most fuel efficient way out of the Solar System?

4 Answers4

Linked