What is the formula to calculate aperture ("diaphragme" in French)?

Question

Let's say I have these data for my camera:

• t : Exposure time in seconds ("temps de pose" in French)
• C : Incident-light meter calibration constant ("constante lumière incidente" in French)
• S : ISO arithmetic film speed
• NDF : Neutral density filter in EV (f-stop) ("filtre à densité neutre" in French)
• EC : Exposure correction in EV (f-stop) ("correction d'exposition" in French)

And this for the environment :

• E : Illuminance of the scene in lux

What would be the formula to calculate N the relative aperture (f-number)?

The question is especially about the filter and correction since without them, N² = E*S*t/C

Answer 1

The equation is:

$$ {N^2\over t} = \frac{E \times S}{C} $$

for \$N=\$ f-number; \$t=\$exposure time (in seconds); \$E=\$ illuminance; \$S=\$ ISO value; and \$C=\$ incident-light meter calibration constant.

Or, \$N^2 = (E\times S\times t)\,/\,C\$, as you've summarized it with \$N\$ as aperture on the left. Note that the calibration constant \$C\$ corresponds to your meter, not to the camera, and usually depends on the shape of the light-receiving surface (flat or dome).

Figure out the aperture and exposure time you need from this, and then adjust these for your neutral density filter and desired exposure compensation. Each 1-unit change in EV is one stop, and you can adjust either exposure time or aperture (or for that matter, ISO) correspondingly.

Or to put it simply: Add together the neutral-density filter EV value (as a positive number of stops) and your desired exposure correction EV value. If the result is positive, widen the aperture by one stop for each correction EV. If the result is negative, narrow the aperture by that amount.

If you want to put this in formula form, that'd be:

$$ N = \left.\sqrt{{E\times S\times t\over C}}\middle/\sqrt{2^{\text{EV compensation}\; +\; \text{ND filter stops}}}\right. $$

There are other ways to arrange the EV compensation and ND filter values, of course, but this representation matches the way a photographer thinks about it — setting the basic exposure parameters and then factoring in the compensation. (You could shift the equation around so the EV compensation and ND filter stops values are in the first √, and probably do want to do that as an optimization.)

It is often the case that the range of adjustable apertures does not give the flexibility one would need for this in the real world. Your lens probably does not go to f/64 or f/1.0. In this case, you'll need to adjust one of the other parameters, of course.

It may help to consider this visualization:

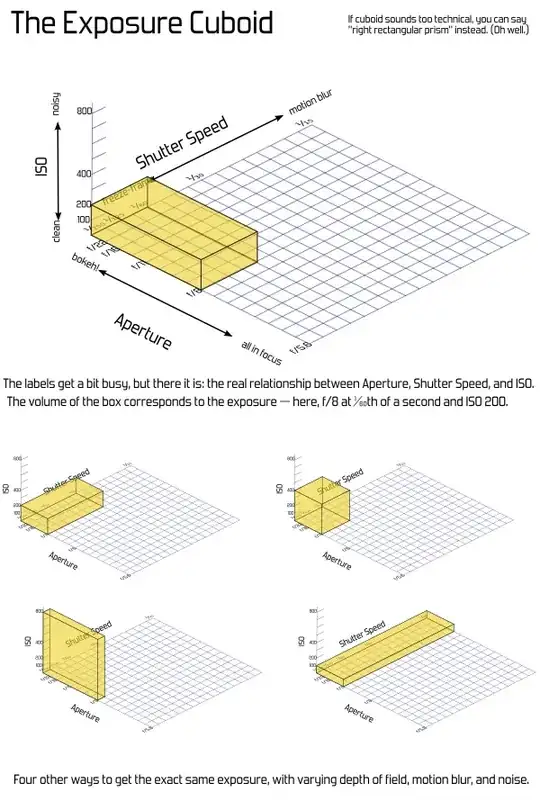
The adjustable exposure parameters on camera are the axes — aperture (f-number), shutter speed, and ISO. The target exposure is the volume of the cube.

Numerically in the basic formula, this volume is determined by the illuminance and calibration constant values. (The "calibration constant" is a value selected to give a nominally-correct overall exposure for a given scene illuminance.)

Exposure compensation is basically you as a human overriding that measurement and increasing or decreasing the target volume. Likewise, adding a ND filter halves the volume (for every stop).

Answer 2

As you know, all optical filters absorb some light hence require an increased exposure to compensate. The magnitude of this increase is universally called the “filter factor”. This value is likely published by the filter manufacturer or you can derive it by making as simple bracketing test.

Once the filter factor is known, we can use it as a multiplier. Suppose a shot of a vista works out to f/16 @ 1/250 of a second. Now you mount a neutral density filter with a filter factor of 8. What is the revised exposure? We calculate by applying the filter factor to the shutter speed thus: 1/125 X 8 = 1/125 X 8/1 = 8/125 = 1/15. If this seems difficult, likely you are a bit rusty when it comes to manipulating fractions.

Table of Filter factors:

Stops of absorption	filter factor
1	2
2	4
3	8
4	16
5	32

They key is: The f-stop is a 2× increment, a doubling of halving of the amount of exposing energy. The basic equation for exposure is \$E=IT\$, where \$E=\$exposure, \$I =\$ the exposing radiation, and \$T=\$the duration of the exposure.

Sorry -- French is Greek to me!

Stated a little differently:

A filter factor is a modifier. Once the filter factor is known, to compute a revised shutter speed, multiply the time of exposure by the filter factor. One can modify the ISO by dividing it by the filter factor. One can modify the f-number by dividing it by the square root of the filter factor.

Filters absorb a quota of the exposing light. It is customary to express the needed correction in terms of f-stops. By custom, the f-stop is defined as a 2× change in exposing energy. Thus a filter that attenuates by 50% requires +1 f-stop compensation. Another way to express this attenuation is via a \$\text{filter factor} = 2^x\$, where \$x\$ is the number of f-stops attenuated. Photo scientists express filter attenuation based on its “opacity” = incident light divided by amount of light that traversed. Optical density is the logarithm (base 10) of the opacity.

f-stop	opacity	filter factor	optical density (O.D.)
1/6	20.16	1.1	0.05
1/3	20.33	1.3	0.10
1/2	20.5	1.4	0.15
2/3	20.66	1.6	0.20
1	21	2	0.30
2	22	4	0.60
3	23	8	0.90
4	24	16	1.20
5	25	32	1.50
6	26	64	1.80