Min Bend Orthogonal Knots

Question

I am seeking literature on 3D orthogonal drawings of knots, especially minimum bend drawings. An orthogonal drawing employs segments parallel to the axes of a Cartesian coordinate system. A bend is a vertex at which two segments meet orthogonally. A drawing insists on simplicity in the sense that nonadjacent segments are disjoint, and adjacent segments meet only at their shared endpoint.

One can imagine first drawing a 2D projection with a minimal number of crossings and then removing the crossings. For the trefoil below, naive crossing-removal increments the $8$ bends in the 2D drawing to $8 + 3 \cdot 4 = 20$ bends, but the trefoil can be drawn with $12$ bends:
          
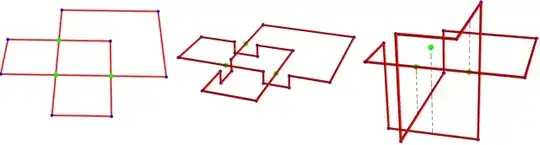
I would be especially interested in algorithmic methods to derive the right 3D drawing above from the left 2D projection. Thanks for ideas and pointers!

Answer 1

Chad Giusti calls these "Plumbers' Knots":

https://arxiv.org/abs/0811.2215

https://arxiv.org/abs/1107.4717

In the first paper Giusti gives the space of plumbers knots a natural stratification which is a CW-decomposition. This allows him to enumerate components of the space (knot types) in a fairly algebraic manner.

---

      ![GiustiFig1][1]
      ^{(Image added by J.O'Rourke)}

---