10

Is there a known algorithm which, given a finite multiset (unordered list) of integers $A$, returns a yes/no answer for "Is there a polyhedron such that the multiset of areas of all its faces is exactly $A$?"?

Is there a known general algorithm for $n$-dimensional polytopes?

Vladimir Reshetnikov
  • 6,709
  • There is one for two dimensions. If you don't mind prisms, you can likely adapt it to arbitrary dimensions. Gerhard "Ask Me About System Design" Paseman, 2011.11.30 – Gerhard Paseman Dec 01 '11 at 01:34

1 Answers1

17

I can answer your question with the specialization to convex polyhedra and polytopes. Specializing further to $\mathbb{R}^3$, the result is that

$n \ge 4$ positive real numbers are the face areas of a convex polyhedron if and only if the largest number is not more than the sum of the others.

I wrote up a short note establishing this: "Convex Polyhedra Realizing Given Face Areas," arXiv:1101.0823. The result relies on Minkowski's 1911 theorem, which perhaps you know:

Theorem (Minkowski). Let $A_i$ be positive faces areas and $n_i$ distinct, noncoplanar unit face normals, $i=1,\ldots,n$. Then if $\sum_i A_i n_i = 0$, there is a closed convex polyhedron whose faces areas uniquely realize those areas and normals.

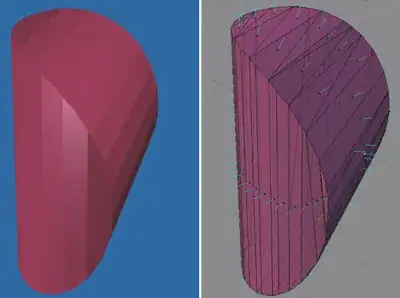
This theorem reduces the problem to finding orientations $n_i$ so that vectors of length $A_i$ at those orientations sum to zero. And this is not difficult. Here is Figure 3 from my note from which you can almost infer the construction:
            Cylinder-Cylinder

Minkowski's theorem generalizes to $\mathbb{R}^d$ and so does an analog of the above claim (but I did not work that out in detail in the arXiv note). In terms of an algorithm, the decision question is linear in the number $n$ of facet areas, and even constructing the polyhedron is linear in $\mathbb{R}^3$, and likely $O(dn)$ in $\mathbb{R}^d$ (but again, I didn't work that out).

But you don't mention the word "convex" in your post, so perhaps you are interested in nonconvex polyhedra and polytopal complexes?

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • Although I did not mention polygons, I suggested such in my comment above. There for n >=3 the condition is the same: no side must have length at least half the sum of all lengths. For arbitrary dimensions, I suspect the same holds true of any nontrivial polytope, convex or not: no k-face has k-measure at least half the sum of the k-measures of all k-faces. Triangular prisms should show that one cannot replace half by anything smaller. Gerhard "Ask Me About System Design" Paseman, 2011.11.30 – Gerhard Paseman Dec 01 '11 at 01:53
  • 4
    Let me mention that in a certain sense, the dual problem was resolved by Zil'berberg in 1962. This paper is not available in English I think, but is stated as Exercise 35.9 in my book: http://www.math.ucla.edu/~pak/book.htm There, the areas are replaced by curvatures, which satisfy the Gauss-Bonnet formula and the proof is via an easy reduction to Alexandrov's "ray theorem", which is dual to Minkowski's theorem (but neither easily implies another). – Igor Pak Dec 01 '11 at 02:16
  • (cont'd) One curious extension of Zil'berberg's proof is that the polytope can be made simple (for even number of vertices). I bet your theorem extends to have all polytopes simpicial. – Igor Pak Dec 01 '11 at 02:17
  • I should be more careful in my statements. Let a polytope live in R^d. For positive integral k less than d there is a constant c_(k,d) such that the sum of the measures of all k-faces of the polytope times that constant is greater than the k-measure of any single k-face. When k=d-1, I assert that the constant is 1/2. For smaller k, smaller constants are possible, and are likely to be c_(k,d)=1/(1+d-k). Gerhard "Ask Me About System Design" Paseman, 2011.11.30 – Gerhard Paseman Dec 01 '11 at 02:17
  • 1
    As a remark to the case of an n dimensional non-convex polytope $P\subset \mathbb{R}^n$, Gerhard's condition is still necessary. Indeed, for any face f , the orthogonal projection onto the hyperplane containing that face is 1-Lipschitz and maps the n−1 skeleton of P minus f surjectively onto f (the easy reason is: f has an inner and an outer side (essentially by hypothesis on P, so that the line orthogonal to f at x∈f also meet ∂P in another y∉f). The analogous argument seems to work also for k-faces (giving the constant 1/2, possibly non optimal) – Pietro Majer Dec 02 '11 at 11:55