Constructing a Polyhedron given areas of its faces

Question

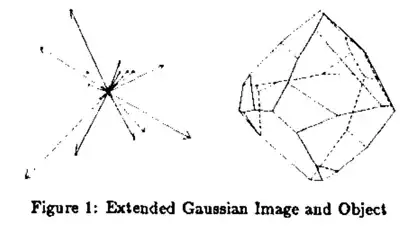
I want to visualize a set of data as a polyhedron in 3d space. Imagine set A includes areas of such polyhedron's faces. I assume the first step is to check if there exist a polyehdron by making sure each area is larger than the sum of other areas. Then we can perhaps find sets of all normal vectors satisfying such polyhedra by solving:

$\sum A_i\cdot N_i=0$

Up to this point the discussion is provided in an earlier post: Building a polyhedron from areas of its faces

I do not know what comes next. Assuming we will settle with a unique set of N (for example one that provides the maximum valume), what are the next steps in constructing the Polyhedron? Also what is the best method to find coordinates of vertices/edges to further interact with the resulting Polyhedron?

On a side note: for designers like me with undergraduate background in Mathematics, what programming language do you recommend to visualize data and models built on mathematical algorithms?

Thanks.

Answer 1

The first effort of which I am aware to reconstruct a polyhedron from the Minkowski theorem data (face areas and normals) is this old paper; but it was a very nice effort, and explicitly computational:

Little, James J. "Determining Object Attitude from Extended Gaussian Images." International Joint Conference on Artificial Intelligence (IJCAI). 1985. (PDF download.)

---

         

---

Later Peter Gritzmann and Alexander Hufnagel published an algorithm for polytopes in arbitrary dimension: "A polynomial time algorithm for Minkowski reconstruction," 1995, Symposium on Computational Geometry. This eventually (1999) became

"On the Algorithmic Complexity of Minkowski's Reconstruction Theorem," Journal London Mathematical Society, Volume59, Issue3, pp. 1081-1100. (PDF download.)

"it is shown that this reconstruction problem can be solved in polynomial time when the dimension is fixed but is #P-hard when the dimension is part of the input."