19

Say that a number is an odd-bit number if the count of 1-bits in its binary representation is odd. Define an even-bit number analogously. Thus $541 = 1000011101_2$ is an odd-bit number, and $523 = 1000001011_2$ is an even-bit number.

Are there, asymptotically, as many odd-bit primes as even-bit primes?

For the first ten primes, we have $$ \lbrace 10, 11, 101, 111, 1011, 1101, 10001, 10011, 10111, 11101 \rbrace $$ with 1-bits $$ \lbrace 1, 2, 2, 3, 3, 3, 2, 3, 4, 4 \rbrace $$ and so ratio of #odd to $n$ is $5/10=0.5$ at the 10-th prime. Here is a plot of this ratio up to $10^5$:

10^5
(Vertical axis is mislabeled: It is #odd/$n$.)

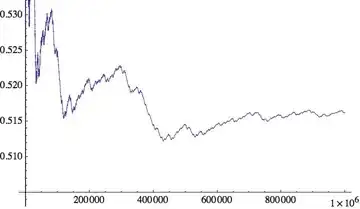
I would expect the #odd/$n$ ratio to approach $\frac{1}{2}$, except perhaps the fact that primes ($>2$) are odd might bias the ratio. The above plot does not suggest convergence by the 100,000-th prime (1,299,709).

Pardon the naïveness of my question.

Addendum: Extended the computation to the $10^6$-th prime (15,485,863), where it still remains 1.5% above $\frac{1}{2}$:

10^6
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 1
    The fact that primes greater than 2 are odd only biases one bit, which should have a negligible effect in the long run. Ignoring the last bit, looking at any particular finite subset of the bits should reveal a uniform distribution by the strong form of Dirichlet's theorem and the difficult question is whether this is still true if one looks at all the bits. – Qiaochu Yuan Nov 02 '10 at 14:58
  • 1
    I guess the 2.5% bias in favor of odd-bit primes in the first 100K is just an unexplainable fact about the distribution...? – Joseph O'Rourke Nov 02 '10 at 15:18
  • 2
    What you call "odd-bit numbers" are often called Thue-Morse numbers. I like your terminology better, but tradition is tradition. – Kevin O'Bryant Nov 04 '10 at 03:08
  • 1
    @Kevin: Thanks for the key phrase! Wikipedia says: "The Thue–Morse sequence was first studied by Eugène Prouhet in 1851,.... However, Prouhet did not mention the sequence explicitly; this was left to Axel Thue in 1906." Quite a long and tangled history! – Joseph O'Rourke Nov 04 '10 at 12:08
  • 8
    I thought the "odd-bit numbers" were usually called odious numbers (and the complementary set called evil numbers). – David Eppstein Oct 31 '11 at 21:51
  • David, I thought the same thing. OEIS agrees with you (http://oeis.org/A000069) and says that the odious numbers are the indices of the 1's in the Thue-Morse sequence (http://oeis.org/A010060). – Michael Lugo Oct 31 '11 at 22:48
  • (Power outtage made my graphs disappear for three days. Sorry!) – Joseph O'Rourke Nov 01 '11 at 14:28
  • Thanks for putting the graphs back up, it makes the question look much nicer! – Charles Nov 08 '11 at 06:21
  • It is still not obvious to me why there is a bias in favour of the odd-bit primes among the first $10^6$ primes. What am I missing? – Klangen Aug 07 '19 at 08:52
  • @JosephO'Rourke I tried, unsuccessfully, to replicate your graph in Mathematica. My results differ significantly from yours; indeed, for instance for $n=20\times10^{3}$, the ratio of odd-bit to even-bit primes is $\frac{10693}{9307}$, i.e., $1.1489\ldots$. Can you explain how you obtained your graph? – Klangen Aug 11 '19 at 16:51
  • @Klangen: I lost my $9$-yr old code, but it was easy enough to recreate. Up to $20000$, I get that exact same fraction. And if you divide #odd by $n$, $10693/20000 \approx 0.53$, which is exactly what the graph shows. I see now that I mislabled the graph as odd/even, when it is odd/$n$, which is why it is close to $\frac{1}{2}$. I will add a remark to correct. – Joseph O'Rourke Aug 12 '19 at 15:30
  • 2
    I believe we have Berlekamp, Conway, and Guy, Winning Ways, to thank for the "odious" and "evil" terminology. – Gerry Myerson Aug 12 '19 at 22:46
  • @JosephO'Rourke Thank you for the clarification, it makes perfect sense now! – Klangen Aug 13 '19 at 05:53

2 Answers2

24

Yes. This was proven in

C. Mauduit and J. Rivat, Sur un problème de Gelfond: la somme des chiffres des nombres premiers, Ann. Math.

I found this by searching for "evil prime" and "odious prime" in the OEIS. More precisely, they prove the Gelfond conjecture:

Let $s_q(p)$ denote the sum of the digits of $p$ in base $q$. For $m, q$ with $\gcd(m, q-1) = 1$ there exists $\sigma_{q,m} > 0$ such that for every $a \in \mathbb{Z}$ we have

$$| \{ p \le x : s_q(p) \equiv a \bmod m \} | = \frac{1}{m} \pi(x) + O_{q,m}(x^{1 - \sigma_{q,m}})$$

where $p$ is prime and $\pi(x)$ the usual prime counting function.

Emil Jeřábek
  • 44,710
Qiaochu Yuan
  • 114,941
21

Yes, the ratio approaches 1/2. This was proven in

C. Mauduit et J. Rivat, Sur un probléme de Gelfond: la somme des chiffres des nombres premiers.

See Three topics in additive prime number theory for exposition. Also, the poorly-named sequences in Sloane: A027697 and A027699.

Charles
  • 8,974
  • 1
  • 36
  • 74
  • 1
    Thanks! There is a nice conjecture of Vladimir Shevelev embedded in the OEIS descriptions: the n-th odius prime is less than the n-th evil prime. I agree that these are poorly named! – Joseph O'Rourke Nov 02 '10 at 16:16
  • 1
    @JosephO'Rourke Indeed. But it seems to me that several of those conjectures are "false", due to Mauduit & Rivat. For example, it cannot be true that A027699(n) - A027697(n) tends to infinity with n. – Klangen Sep 26 '22 at 06:37
  • @Klangen Perhaps you could submit that as a comment to those sequences? – Charles Sep 26 '22 at 15:25