Parity of primes

Question

While working on a completely different (combinatorial) problem, I ran a simple program to calculate the parity of the first ~50000 primes (number of 1s in their binary representation modulo 2). The following graph summarizes the result:

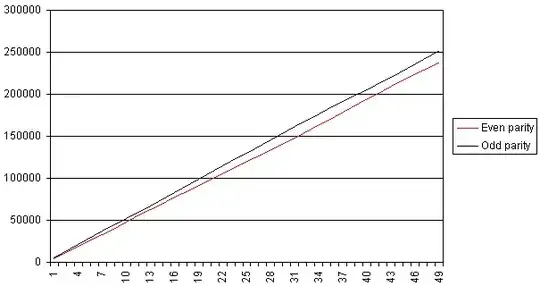
enter image description here

The number of primes having even parity seems to grow slower.

Is there a math explanation ?

I looked to the correspoding OEIS entry, but it doesn't provide any detail.

What does "parity" mean? The parity of the number of ones in the binary representation? If so, please say it. If not, please say it. — Igor Rivin, Oct 22 '14 at 18:46
@IgorRivin: sorry, question edited (I had only one non-trivial definition of parity of a number in my mind :-) — Marzio De Biasi, Oct 22 '14 at 18:54
It's right there on the right hand side under "Related". http://mathoverflow.net/questions/44561/odd-bit-primes-ratio — Felipe Voloch, Oct 22 '14 at 18:57
@FelipeVoloch: thanks, I didn't notice it while typing the question (or perhaps it wasn' there) :-S ... a.k.a. the Thue-Morse numbers ... — Marzio De Biasi, Oct 22 '14 at 19:00
A version of this question was earlier explored in "Odd-bit primes ratio." — Joseph O'Rourke, Oct 22 '14 at 19:36
@NateEldredge: y axis: number of primes having even (red line) or odd (black line) parity; x axis: number of primes considered (in thousands) — Marzio De Biasi, Oct 22 '14 at 21:45

score 7 · Accepted Answer · answered Oct 22 '14 at 18:55

7

It was shown (amongst other things) by Gel'fond that the asymptotic growth rates of the primes with even and odd parity base 2 expansions are the same:

Gelʹfond, A. O. Sur les nombres qui ont des propriétés additives et multiplicatives données. (French) Acta Arith. 13 1967/1968 259–265.

A more recent paper on this is due to Mauduit and Rivat.

answered Oct 22 '14 at 18:55

Anthony Quas

22,470

14

I've noticed that most primes seem to start with a 1 in their base 2 expansion. – Anthony Quas Oct 22 '14 at 18:58
OK, so, asymptotically they are the same, but that doesn't rule out the possibility that odd parity up to $N$ exceeds even for all $N$. It doesn't even exclude the possibility that the difference goes to infinity. Do the published results speak to these more delicate questions? – Gerry Myerson Oct 22 '14 at 22:16
1

It is known that among multiples of 3, asymptotically half of them have an even number of 1s in their binary expansion, but there is a second-order term that biases multiples of 3 towards having an even number of 1s. (At its core, this is because a multiple of 3 must have its alternating sum of bits be a multiple of 3; this is more likely when there are the same number of even-bit 1s and odd-bit 1s than when there are 3 more even-bit 1s than odd-bit 1s, etc.) ... – Greg Martin Oct 22 '14 at 22:32
... Presumably then, the bias in the above graph is due (to first-order approximation) to the fact that primes are not multiples of 3. This phenomenon has been explored by V. Shevelev (see papers on the arXiv). – Greg Martin Oct 22 '14 at 22:32
It seems too that most primes end with a $1.$ It is rare to have all $1's$ but even rarer to only have that pair of $1$s..... – Aaron Meyerowitz Oct 23 '14 at 07:52

Parity of primes

1 Answers1