16

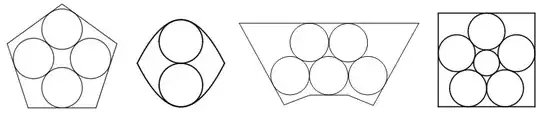
Circular coins in a frame may all be stuck in their positions; for example:

enter image description here

Another possibility is that they can all move simultaneously; I claim the following examples:

enter image description here

It is not always obvious that the coins can move, and it can be quite tedious, or nearly impossible, to show algebraically that the coins can move. We can use animations (example1, example2, example3), but that's not quite rigorous.

Are there general principles that allow us to easily determine whether coins in simple arrangements in a frame can all move?

Here are some of my attempts at formulating such general principles.

  • Earlier I conjectured that if circular coins of any sizes are in a convex polygonal frame, with each coin touching exactly one edge, then all the coins can move. A counter-example, using coins of different sizes, was given.
  • Then I proposed a second conjecture that was like the first one, except it required the coins to be equal size. A counter-example was given.
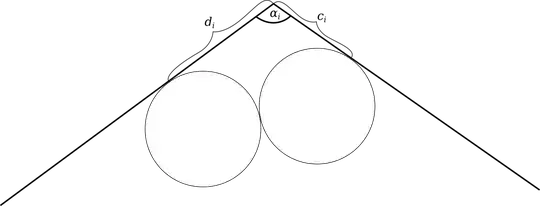
  • My latest idea is to add the condition that the coins must be in a ring (i.e. every coin touches exactly two other coins), but I would not be surprised if there's yet another counter-example.

Anyway, I open to floor to general principles that are useful in determining if coins in simple arrangements in a frame can move.

(I have no strict definition of "simple arrangements". Let's say, just a few coins, and just a few sides and/or "natural" curves like circular arcs, parabolas, etc. I exclude arrangements in which a coin can move without disturbing others, and arrangements in which the coins can rotate as a single rigid body about a fixed point.)

Dan
  • 2,431
  • 2
    As should be clear from the previous answers at https://mathoverflow.net/a/438315/36721 and https://mathoverflow.net/a/438403/36721 , the problem is actually a linear programing one, of a certain kind. It is unclear to me, though, if it being of such a kind helps. – Iosif Pinelis Jan 12 '23 at 19:15
  • 3
    This paper of Robert Connelly may be relevant: https://dl.acm.org/doi/abs/10.1016/j.ejc.2008.01.009 as well as the paper by Baryshnikov, Bubenik and Kahle which introduces a min-type Morse theory for hard sphere configuration spaces: https://arxiv.org/pdf/1108.3061.pdf – Mark Grant Jan 13 '23 at 10:55

1 Answers1

8

With a ring configuration in a convex polygon and no coin touching two walls, they can always move.

Without loss of generality, assume that each wall has a coin on it. (Walls not touched by any coin have no impact to small movements and can thus be omitted, extending the polygon.) It is sufficient to consider movements along the walls. (If other movements are possible, the problem is trivial.)

The situation thus boils down to a chain of touching-points of the following appearance:

Single-corner reduction

Proposition 1: $c_i$ and $d_i$ are in a strict-monotonically decreasing relationship to each other.
This is actually not true in general: specifically, for acute $\alpha_i$ we can have the situation where both coins move simultaneously further into the corner. This case can however be disregarded, because it immediately provides a solution, namely just move these two coins.

Lemma 2: $L_i := c_i+d_i$ is concave (considered as a function of either $c_i$ or $d_i$), regardless of $\alpha_i$.
The proof is left as an exercise.

Furthermore, in the degenerate case $\alpha_i=180^\circ$, $L_i$ is constant and thus still (non-strictly) concave; this covers the case that multiple coins touch the same wall.

Now consider the chain of coins, numbered from $i=0$ to $i=n-1$, to stay connected. $d_i + c_{i+1}$ is constant (namely the length of that side of the polygon); together with proposition 1 this implies that the movement of all the coins together can be parameterised equivalently by any of the $c_i$.

If I say “all coins”, we're treating the $i=0$-coin as split in two halves here, each of them touching only one other coin and still staying tangential to the wall. The distance between the halves of this split coin, considered as a function of moving the whole chain, is a constant (the polygon circumference) minus a sum of concave functions by lemma 2 (the $L_i$ contributions, using the fact that a concave function composed with a monotonically increasing one is still concave), and is therefore a convex function. Consequently, it is possible to move the whole chain in at least one direction without pressing the two halves of the $i=0$ coin into each other. Or equivalently, all coins (no splitting) can move in at least one direction without pressing two coins into each other.

I am almost sure that the condition of the polygon to be convex can be dropped: although $L_i$ fails to be concave at an impinging vertex, the other corners have to be all the more acute in this case and have therefore more strongly concave $L_i$. But it is more elaborate to show that the whole sum is concave then.

leftaroundabout
  • 213
  • 1
    (i) What is a "a ring configuration"? (ii) What is "a function of moving the whole chain"? (iii) Why do you only consider "The distance between the halves of this split coin"? What about the distances to the other coins? (iv) Why does "therefore a convex function' imply "Consequently, it is possible to move the whole chain in at least one direction". Etc., etc. Can you just give a formal answer? – Iosif Pinelis Jan 12 '23 at 20:04
  • 3
    (ⅰ) Is defined in the question. (ⅲ) The other coins are permanently touching, which defines (ⅱ) what movement of the whole chain must be. (ⅳ) Convexity of the split-distance means that at most one direction of movement would turn it negative (which must not happen); the other direction either leaves all distances zero or creates a gap somewhere. — Making the answer formal would require introducing explicit parameters for the displacement of each coin from its original position. It's possible, but it would be a lot longer, and t̶h̶i̶s̶ ̶m̶a̶r̶g̶i̶n̶ ̶i̶s̶ ̶t̶o̶o̶ ̶n̶a̶r̶r̶ow̶ I don't have time. – leftaroundabout Jan 12 '23 at 21:21
  • @leftaroundabout Does your general principle require that the coins are all the same size? – Dan Jan 13 '23 at 10:15
  • 1
    @Dan yes, because there's another implicit lemma that $c_i$ and $d_i$ have to be strictly monotone decreasing as functions of each other, and that doesn't hold for general non-equal coins. Though again, I suspect this condition could be weakened but it would make the maths much more difficult. – leftaroundabout Jan 13 '23 at 10:18
  • I edited to make this lemma explicit. – leftaroundabout Jan 13 '23 at 10:24
  • 1
    Uh, wait a moment... this isn't even true for equal-sized coins! I think there's a flaw in the argument there! – leftaroundabout Jan 13 '23 at 10:28
  • 2
    Scratch the last comments, the non-monotonic case is actually another trivial solution, so we don't need to worry about that. – leftaroundabout Jan 13 '23 at 11:55
  • Nice work. In the OP I showed a trapezium with four coins. I wonder if there is a general principle that tells us that those coins can move (Here is a desmos graph that shows that they can move.) – Dan Jan 13 '23 at 12:55
  • 1
    Well, the coins on the top and bottom in the trapezium can move past each other as if they weren't touching at all, so this still works by the same principle as a 2-neighbours chain. – leftaroundabout Jan 13 '23 at 13:03
  • Could your principle apply to curved edges, like the quarter-disk in the OP? Maybe regard a curve as a polygon with an infinite number of edges, with some restrictions on curvature? – Dan Jan 13 '23 at 13:36
  • Maybe. Explore by proving the lemma and see whether that can be generalized. But first I'd look for some more counterexamples. Fairly sure it's not enough to require the curvature to be less than the circles' curvature. – leftaroundabout Jan 13 '23 at 13:52
  • 1
    @leftaroundabout In "Proposition 1", I don't understand "both coins move simultaneously into the corner". How is that possible? – Dan Jan 14 '23 at 01:54
  • @Dan well, at first I thought it wasn't possible (which is what proposition 1 says). But actually it is: consider a very acute corner, so that both lines are almost parallel where the coins are. – leftaroundabout Jan 14 '23 at 09:48
  • @leftaroundabout I'm still not getting it. Say there are equal size circles in a tight corner of just 1 degree. I don't think the circles can move simultaneously into the corner. If one of the circles moves towards the corner, the other must move away from the corner. Perhaps I am missing something? – Dan Jan 17 '23 at 01:13
  • Well, try it out with actual coins! – leftaroundabout Jan 17 '23 at 08:15