15

Earlier I conjectured that if circular coins of any sizes are in a convex polygonal frame, with each coin touching exactly one edge, then all the coins can move. A counter-example using coins of different sizes was given.

Here is a new conjecture that avoids that counter-example:

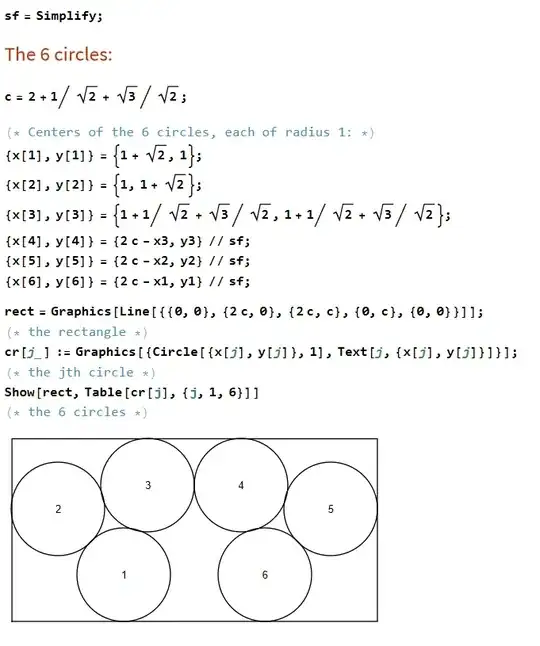
If equal size circular coins are in a convex polygonal frame, with each coin touching exactly one edge, then all the coins can move.

Is my new conjecture true?

EDIT

EdwardH has found a counter-example. I have asked another question asking for general principles that are useful in determining whether coins can move.

Dan
  • 2,431
  • I am a bit confused. Take two regular triangles and assemble them into a rhombus. Now, take the configuration of four coins with centers at the vertices of the rhombus and diameters equal to the side of the rhombus. Suppose these coins are now tightly bound by the rectangle who sides are parallel to the diagonals of the rhombus. Presumably this is a counterexample? – Vladimir Dotsenko Jan 12 '23 at 07:05
  • @VladimirDotsenko In the arrangement you described, consider the group of four coins as a single rigid body. You can rotate it about its centre within the frame (but not a full revolution). – Dan Jan 12 '23 at 07:39
  • 11
    Can these coins move? https://imgur.com/a/ivQfMky – Edward H Jan 12 '23 at 08:00
  • What about these four coins in a rhombus? https://ibb.co/GsYkqx4 – Alessandro Della Corte Jan 12 '23 at 10:30
  • 3
    @AlessandroDellaCorte I believe those can move. Here is a desmos graph. – Dan Jan 12 '23 at 10:57
  • 2
    Yep! Thank you. Concerning the potential counter-example by Edward H, I notice that there the coins are more than the sides of the frame. Maybe the conjecture still holds when they are at most equal in number? – Alessandro Della Corte Jan 12 '23 at 11:02
  • 7
    @EdwardH I'm convinced that your counter-example is valid. It's two mirror images of the most efficient packing of three circles in a square (see for example www.packomania.com). Call the two circles at the bottom A and B, with A on the left. If A moves, its initial direction must have a positive rightward component, but that would push B to the right, which is impossible. If you post your counter-example as an answer, I would accept it. – Dan Jan 12 '23 at 11:15
  • 3
    @AlessandroDellaCorte Can’t you just split the two long sides (and perhaps move the segments a little, if you don’t want sides to be colinear)? Or alternatively, bevel the corners? – Emil Jeřábek Jan 12 '23 at 12:30
  • @EmilJeřábek yes, maybe a more sensible approach is to ask that each coin touches exactly one side and vice-versa. Do you think you can achieve that by splitting the long sides without allowing some degree of freedom? – Alessandro Della Corte Jan 12 '23 at 16:12
  • Well I haven’t done anything more rigorous than eyeballing, but yes, I think so. – Emil Jeřábek Jan 12 '23 at 17:04

1 Answers1

12

This is to confirm that the suggestion by Edward H is valid.

The specific calculations have been done in a Mathematica notebook, whose image is below. I think the notebook contains all the necessary comments:

enter image description here

enter image description here

Iosif Pinelis
  • 116,648