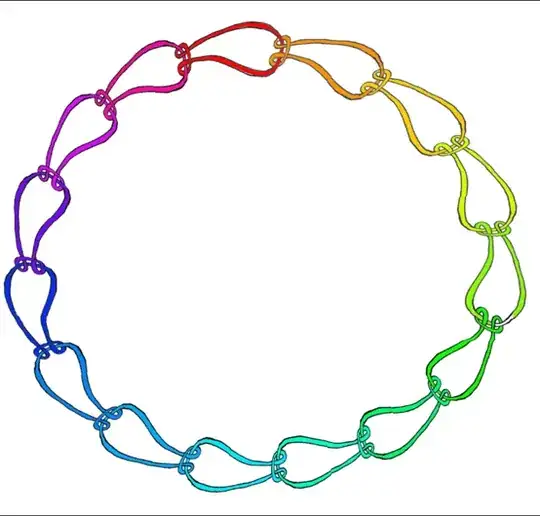
The attached image shows a way to construct an $n$-component Brunnian link for any $n\geq 3$. That is, this link is not trivial, but deleting any of its components makes the new link trivial. The latter property is obvious from the picture, however I would like to have a strict proof of nontriviality. What bothers me is that nowhere in the literature there is an example of proving nontriviality of any Brunnian $n$-link.
Let us denote this link by $L=K_1\cup K_2 \cup \dotsb \cup K_{n-1}\cup K_n$. Also, it might be useful to examine $L'=L\setminus K_n=K_1\cup K_2 \cup \dotsb \cup K_{n-1}$. I tried to look at the link group $\pi_1(L').$ Since $L'$ is equivalent to $n-1$ disjoint circles, I conclude that $\pi_1(L')=F_{n-1}$. Then I ask what $[K_n]\in \pi_1(L')$ would be in the case if $L$ were trivial. In that case I would be able to move $K_n$ a little bit and get a homotopic loop that is a clean circle, thus $[K_n]\in \pi_1(L')$ is the identity. Now, for contradiction I would like to calculate explicit form of $[K_n]\in \pi_1(L')$ (or to somehow just prove that it is not the identity). I tried doing it with Wirtinger presentation, but it was messy and, even if I did find explicit form for $[K_n]\in \pi_1(L')$ in terms of group’s generators correctly, determining whether $[K_n]$ is equal to the identity in this finitely generated group is a well-known undecidable problem.
Is there a way to improve my approach in order to prove nontriviality? If not, do you see another way to prove that? Actually, just an example of proof of nontriviality for any $n$-component Brunnian link would be enough for me, chances are the idea would work for many Brunnian links if not for all.