48

Is there a nontrivial link in a big solid torus that is trivial in the ambient Euclidean space such that each circle is unknot and has a sufficiently small length?

It is motivated by a question that bothers me from my childhood:

Is it possible to wrap a suitcase with hair ties without tying them together?

enter image description here

Comments

  • The answer of Larsen Linov is accepted, but it remains to prove formally that the link meets the conditions. The latter is equivalent to nontriviallity of the following link; the example of Larsen Linov (or a similar one) can be obtained by stating that one of circles is a meridian of the solid torus.

picture from here https://math.stackexchange.com/questions/4338772/is-this-object-a-simpler-brunnian-rubberband-loop-than-those-studied

  • Another question: is it possible to do the same with large rotational symmetry?
Sam Nead
  • 26,191
Anton Petrunin
  • 43,739
  • 5
    I don't have an answer, but the term "rubberband Brunnian link" seems relevant. – Timothy Chow Jun 07 '22 at 22:38
  • 4
    If this were possible then every nine-year old with a rubber band loom would know about it… – Sam Nead Jun 08 '22 at 02:14
  • 1
    Doesn't Kanenobu's papers on links with Brunnian properties answer your question? – Ryan Budney Jul 10 '22 at 23:55
  • 4
    Here is a geometric proof. Let $L_n$ be the rainbow link you drew. Then $L_n$ is a "meridional" Dehn filling of a cyclic $n$-fold cover of a two-component ten-crossing hyperbolic link (called L10n36 by SnapPy). These two components are, respectively, the unknot and the connect sum of a left and right trefoil. Since the meridional slope of the unknotted component grows linearly with $n$ we may apply Thurston's hyperbolic Dehn filing and deduce that all but finitely many of the $L_n$ are hyperbolic. – Sam Nead Jul 11 '22 at 08:45
  • 2
    Nicest question of the year!! Isn't there a badge for that? i think I'll do this question in all my topology-based dissemination :) – Andrea Marino Jul 11 '22 at 21:31
  • 6
    This question now has a great YouTube video by Henry Segerman, Sabetta Matsumoto, and Saul Schleimer at https://youtu.be/Cyhqc8l03GE . – Mark S. Jun 29 '23 at 00:41

2 Answers2

26

This configuration should work:

hair ties solution

Edit (to provide credit/context): Michael Freedman's solution (see Ian Agol's post) is the original one. Ian directed me to this problem and gave me the hint that Michael had already confirmed it was possible.

Larsen Linov
  • 356
11

I shared this question with Michael Freedman who came up with a solution similar to Larsen’s and asked me to post on his behalf.

Michael Freedman's solution

He made a physical realization too.

hair ties

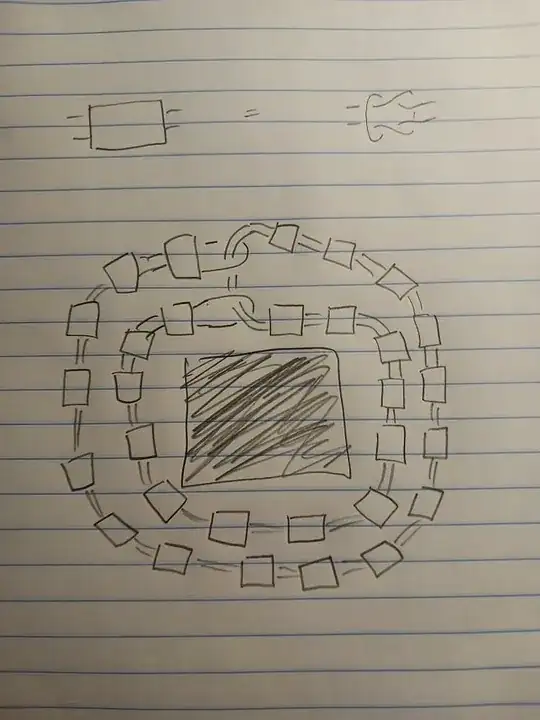
I’ll address Anton’s question of how to prove that this is not the unlink. There is a general method of Haken and Waldhausen to show that manifolds are Haken, and hence have incompressible boundary (in which case they cannot have an unknot component). Exhibiting a simple hierarchy can prove that a manifold is Haken. One can show that the handlebody Freedman embeds has incompressible complement in the solid torus by exhibiting a simple hierarchy. The first stage is annuli going around the loops. After that it becomes compressible, and the next stage of the hierarchy is a compressing disk. The last stage is torus × I, and one can finish off with a hierarchy for this with annuli and disks. Inside the handlebody (at the top of the diagram), the link is also essential. There are a variety of hierarchies one could use here: first use 4-punctured disks to break it up into pieces of finitely many types (most of which look like the box in Larsen’s picture), then analyze each of these finitely many pieces. Hopefully this gives a flavor of how these certificates behave.

Addendum: Okay, I see what Anton is saying now. Larsen’s (or Mike’s) configuration is equivalent to:

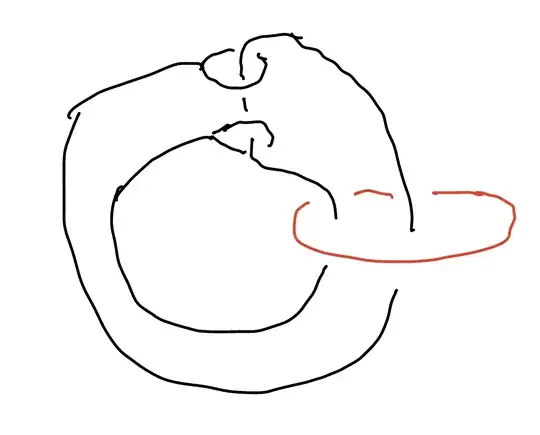
Equivalent configuration

This can be deformed to:

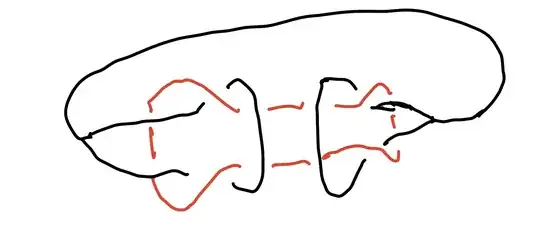
Deformed configuration

Inserting the Brunnian chain pattern into here gives the link shown in Anton’s comment, which Sam Nead proves is a non-trivial link in the comments.

LSpice
  • 11,423
Ian Agol
  • 66,821
  • 3
    It might be more helpful to later readers to instead write “which Sam Nead proves”. :) – Sam Nead Jul 11 '22 at 18:45
  • 2
    @LSpice thanks for this, we were probably editing at the same time, but you finished first. Go ahead and re-edit if you like, or I’ll have a look when I get a chance. – Ian Agol Jul 11 '22 at 20:22
  • 2
    I have re-made the edit, and made the Saul → Sam Nead change, as well as linking the relevant proof. You reference "the link shown in Anton's comment", but I couldn't find that one, so didn't link it (different meanings of 'link' ). – LSpice Jul 11 '22 at 20:33
  • 2
    @LSpice In the comment he added in his answer, he has a picture of a rainbow colored link. I’m proving that Larsen’s example is isotopic to his (which clearly Anton already knew). – Ian Agol Jul 11 '22 at 20:35
  • 1
    Not being familiar with this method of Haken and Waldhausen, it's not clear to me: what is the minimal number of components of the link such that this works? Of course one component doesn't work -- does it work with two components? – Tim Campion Jul 11 '22 at 21:06
  • 1
    @TimCampion this method works for knots too, but one needs to start with a Seifert surface. This is the basis of a recent algorithm of lackenby to detect the unknot in quasipolynomial time. I thought I would try to describe it in this case since one can see many of the surfaces in the hierarchy explicitly. But without diagrams it is hard to communicate. Sam Nead‘s approach is more direct, but uses the more sophisticated (historically) method of hyperbolic Dehn filling. – Ian Agol Jul 11 '22 at 22:22
  • @IanAgol Thanks -- to clarify, I meant to ask not about the general method, but rather: What is the minimal number of connected components of a link (with each component unknotted) in a solid torus which becomes unlinked in the ambient Euclidean space? Your pictures seem to have two connected components, but I'm not sure if that means the answer is 2 (your pictures are not pictures of manifolds, so I gather they are pictures of some sort of intermediate stages in one of theses "hierarchies", and for all I know components can merge there...). – Tim Campion Jul 11 '22 at 22:31
  • @TimCampion the eyeglass shape is meant to be the handlebody in the figure that Mike Freedman drew. Inside of there is the link shown in top of his diagram. As the eyeglass shape is isotopes, the link inside it gets isotoped. – Ian Agol Jul 12 '22 at 02:52
  • @IanAgol Ah, I see. So from the writing in Freedman's drawing, I gather that the upper bound we have here is $n=100$ connected components? – Tim Campion Jul 12 '22 at 13:44
  • 1
    @TimCampion no, in fact you can use two components, the borromean rings is an example. The point he is trying to make is that when the length is very small, there will be a large number of components, say 100 for example. – Ian Agol Jul 12 '22 at 14:12
  • @IanAgol I thought one of the parameters was that the link should come unlinked in the ambient Euclidean space -- but the Borromean rings are linked in the ambient Euclidean space, right? And the Borromean rings have 3 connected components right? – Tim Campion Jul 16 '22 at 11:32
  • I meant use one the complement of one of them as the solid torus. – Ian Agol Jul 16 '22 at 14:04