Understanding conditional entropy intuitively $H[Y|X=x]$ vs $H[Y|X]$

Question

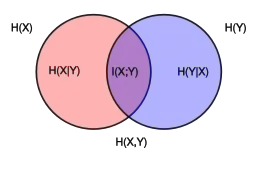
I was trying to understand conditional entropy better. The part that was confusing me exactly was the difference between $H[Y|X=x]$ vs $H[Y|X]$.

$E[Y|X=x]$ makes some sense to me intuitively because its just the average unpredictability (i.e. information) of a random variable Y given that event x has happened (though not sure if there is more to it).

I do know that the definition of $H[Y|X]$ is:

$$H[Y|X] = \sum p(x) H(Y|X =x) $$

But I was having trouble interpreting it and more importantly, understanding the exact difference between $H[Y|X=x]$ vs $H[Y|X]$.

Answer 1

Consider two random variables $X$ and $Y$. If $X=1$ we know that $Y$ is also equal to one. So we do not have any uncertainty about $Y$ knowing that $X=1$. In this sense: $$ H(Y|X=1)=0 $$ Now the question is: How uncertain are we about $Y$ if we know the realization of $X$? First of all, $H(Y|X=1)=0$ only tells us that we do not have any uncertainty about $Y$ only when we know that $X=1$. But for another $X$, for instance if we know that $X=2$, we may not know exactly about $Y$, which means that: $$ H(Y|X=2)>0. $$ Note that, we are looking for a value representing uncertainty of $Y$ if we know $X$. One option is to take the average of uncertainty that we have about $Y$ knowing each $X=x$, which gives us the notion of conditional entropy.

The notion represents the average uncertainty that we have of $Y$ knowing $X$. A good property of conditional entropy is that if we know $H(Y|X)=0$, then $Y=f(X)$ for a function $f$.

---

To see another interest behind the conditional entropy, suppose that $Y$ is an estimation of $X$ and we are interested in probability of error $P_e$. If for $Y=y$, we can estimate $X$ without error then $H(Y|Y=y)=0$. Interestingly, we can use Fano's inequality to find a lower bound on probability of error: $$ H(X|Y)\leq P_e\log(\|\mathcal X\|)+1. $$ And here the conditional entropy gives us an inner bound on the probability of error.

Answer 2

It's intuitive to interpret $H(Y|X)$ by the chain rule:
$$H(Y|X)=H(X,Y)-H(X)$$

Assume that the combined system determined by two random variables X and Y has joint entropy $H(X,Y)$, that is, we need $H(X,Y)$ bits of information on average to describe its exact state. Now if we first learn the value of $X$, we have gained $H(X)$ bits of information. Once $X$ is known, we only need $H(X,Y)-H(X)$ bits to describe the state of the whole system.

And the difference can be also found in Wikipedia:

If $H(Y|X=x)$ is the entropy of the discrete random variable $Y$ conditioned on the discrete random variable $X$ taking a certain value $x$, then $H(Y|X)$ is the result of averaging $H(Y|X=x)$ over all possible values $x$ that $X$ may take.

Answer 3

There is a beautiful explanation of this in the wikipedia page for conditional entropy under motivation.
$$H(Y\mid X)=\sum_x p(x) H(Y\mid X=x)$$ That is, we want the weighted average. Here's where it becomes interesting because $$H(Y\mid X=x)=-\sum_y p(y\mid x)\log p(y\mid x)$$ With $p(y,x) = p(y\mid x)p(x)$ this gives us: $$H(Y\mid X)=-\sum_{x,y} p(y,x)\log\frac{p(x,y)}{p(x)}$$ I kept thinking well why is it not just: $$-\sum_{x,y}p(y\mid x)\log p(y\mid x)$$ Because it is the weighted sum, not the sum.

Answer 4

There is some information since you don't know the value of $X$, so

$$ H[Y|X=x] \leq H[Y|X] = \sum p(X=x) H[Y|X=x] \leq H(X,Y)$$ Merely knowing that $X$ has taken some value, lowers the amount of information you learn from $Y$.

It is certainly lower than the joint entropy of $X$ and $Y$.

$$H(X,Y) = \sum p(x,y) \log p(x,y) $$

---

If this were conditional expectation you'd have the linearity of expectation. Knowing that $X$ takes some value doesn't change your expection.

$$ \mathbb{E}[Y|X] = \sum p(x) \mathbb{E}(Y|X =x) = \mathbb{E}[Y] $$