Solving an initial value problem - PDE

Question

I have to solve $u_{tt}-u_{xx}=0$ with the given I.C.s

\begin{cases} u_x(0,t)=u_x(\pi,t)=0\\ u(x,0)=\cos x \\ u_t(x,0)=-\cos x \end{cases}

Solving the PDE with separation of variables : \begin{equation} \begin{array} e-\frac{1}{X}u_{xx}=-k^2 \\ \frac{1}{T}u_{tt}=-k^2 \end{array} \end{equation}

which give the following solutions: \begin{gather} u(x,t)= \begin{cases} Ae^{kx}\cos kt\\ Ae^{-kx}\cos kt \\ Ae^{kx}\sin kt\\ Ae^{-kx}\sin kt \end{cases} \end{gather} Given the I.C. nr 2, I can see that the solution must have the cosine term, so I disregard the sine solutions. Then, since this is an oscillatory problem, I disregard the solution with $e^{kt}$ since $e^{kt}\rightarrow \infty$ (since this is not a perturbed system ). I am left with

\begin{equation} u(x,t)= Ae^{-kx}\cos kt \end{equation}

When I want to find A, I use I.C. 2:

\begin{equation} cosx= Ae^{-kx}\cos 0t \rightarrow A=\cos xe^{-kx} \end{equation}

This gives

\begin{equation} u(x,t)= \cos x\cos kt \end{equation}

But from here, I am not sure about $k$. If I use the other conditions, I just get $0=0$ or I use the third IC:

\begin{equation} \begin{array} fu_t(x,t)= -k\cos x\sin kt\\ IC: u_t(x,0)=-\cos x:\\ -\cos x= -k\cos x\sin 0\\ \frac{1}{k}=0\\ k=0? \end{array} \end{equation}

This gives

\begin{equation} u(x,t)= cosx \end{equation}

However, this is a strange result, since the PDE is for a function $u(x,t)$, having only one variable. Is there an apparent error here?

Thanks

UPDATE:

Separation of variables was not properly written:

Solving the PDE with separation of variables : \begin{equation} \begin{array} e\frac{1}{F}F_{xx}=k^2 \\ \frac{1}{T}T_{tt}=k^2 \end{array} \end{equation}

which gives the two ODEs:

\begin{equation} \begin{array} eF_{xx}-Fk^2=0 \\ T_{tt}-Tk^2=0 \end{array} \end{equation}

with the solutions:

\begin{cases} Ae^{kx} \\ Ae^{-kx}\\ Be^{kt}\\ Be^{-kt} \end{cases}

Here we can disregard from the positive exponentials, and have:

$u(x,t)=Ae^{-kx}Be^{-kt}$ which we can write as:

$u(x,t)=Ae^{-k(x+t)}$

$u_t(x,t)=-Ake^{-k(x+t)}$

$u_x(x,t)=-Ake^{-k(x+t)}$

Using second IC:

\begin{equation} \begin{array} f u(x,t)=Ae^{-k(x+t)}\\ IC: u(x,0)=\cos x \\ Ae^{-kx}=\cos x \\ A=e^{kx}\cos x \end{array} \end{equation}

So we have now $u(x,t)=e^{kx}\cos x e^{-k(x+t)}\rightarrow \cos x e^{-kt}$

Therefore: $u(x,t)= \cos x e^{-kt}$

We find k by the 3d IC:

\begin{equation} \begin{array} f u(x,t)= \cos x e^{-kt}\\ IC: u_t(x,0)=-\cos x \\ -k\cos x e^{0}=-cosx\\ k= 1 \end{array} \end{equation}

So the final answer is:

\begin{equation} u(x,t)= \cos x e^{-t} \end{equation}

A double check show that this is correct:

\begin{equation} \begin{array} fu_{xx}(x,t)= \cos x e^{-t} \\ u_{tt}(x,t)= \cos x e^{-t} \\ u_{tt}-u_{xx}=\cos x e^{-t}-\cos x e^{-t}=0 \end{array} \end{equation}

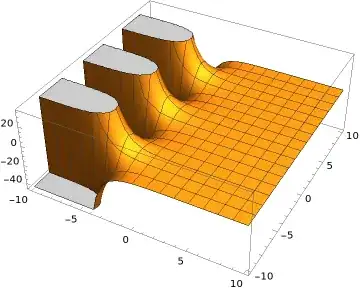
So the original problem $u_{tt}-u_{xx}=0$ is satisfied by $u(x,t)= \cos x e^{-t} $.

A plot of $u(x,t)$ is given below

Answer 1

This problem can be solved using separation of variables. Setting $u=X(x)T(t)$ gives $$ \frac{T''}{T}=\lambda = \frac{X''}{X},\;\; X'(0)=X'(\pi)=0. $$ The solutions are $X_n(x)=\cos(n x),\;T_n(t)=A_n\cos(n t)+B_n\sin(n t)$, which correspond to $\lambda_n=-n^2$ for $n=0,1,2,3,\cdots$. So the general solution may be written as $$ u(t,x)=\sum_{n=0}^{\infty}(A_n\cos(n t)+B_n\sin(n t))\cos(n x). $$ The initial conditions are $$ u(0,x)=\cos(x),\;\; u_{t}(0,x)=-\cos(x). $$ The first condition determines the $A_n$'s and the second determines the $B_n$'s: $$ \cos(x)=\sum_{n=0}^{\infty}A_n\cos(n x),\;\; \cos(x)=\sum_{n=1}^{\infty}B_nn\cos(n x) $$