The paradox is given in the chap. 1 of the book titled : Mathematical Fallacies and Paradoxes, by Bryan Bunch; as given here.
The book explanation has no mathematical formulation, say if states the path in terms of cycloid (also shown in Fig. 1.5, on page #7); then there is no formula for the same.
Also, using that the nearly flattened ends of the curve for inner circle's point B could have been given a mathematical explanation.
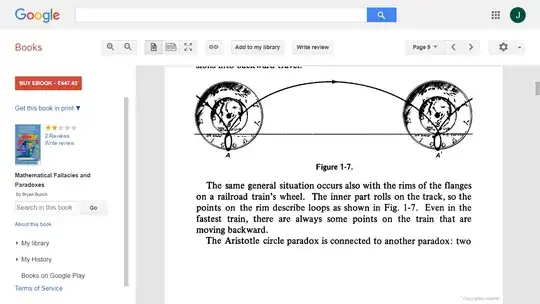
Further, there should be some mathematical explanation & quantification for the reverse loop attained by the fastest point on the rim, as shown in Fig. 1.7 on page #9, as also shown below.
Also, I am not clear if the reverse path is restricted to only the fastest point, or decreases quantitatively with each inner point till the center.