3

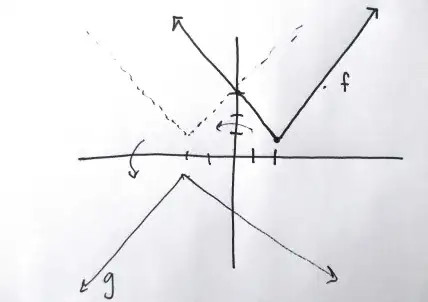
The problem is taken from the chap. 1.1 of the book titled : Calculus Problems for the new century, by Robert Fraga.

A function $f$ has values $f(0) =3, f(2)=1$, is piecewise linear, & has the slope $-1$ if $x\lt 0$ and $1$ if $x\gt 2$. Sketch the graph of the function $g$ defined by each of the following rules.

a.$\,\,\,g(x)=f(x)$
b.$\,\,\,g(x)=-f(-x)$
c.$\,\,\,g(x)=f(x+2)$
d.$\,\,\,g(x)=f(2x)$
e.$\,\,\,g(x)=f(3x-6)$

I have prepared solutions, which are not matching in part (b) (& have confusion for part (e)) with the book's solutions, which are given in terms of graphs.

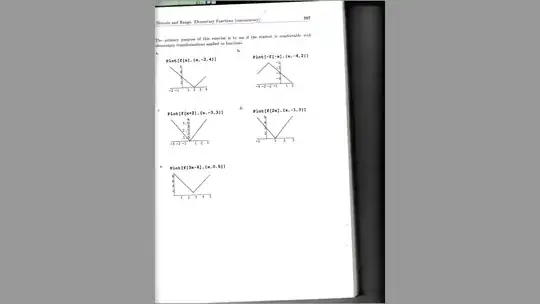
The book's solutions are shown below: enter image description here

My solutions:
I assume that the curve is connected between the points $x=0$ and $x=2$.
The equation of the curve will be given by :

Part (a):
(i) $y = -x+3,\,\,\, x\le 2$
(ii) $y = x-1,\,\,\, x\gt 2$

For Part (b), my graph is wrong, as per the solution given.
Part (b):
(i) $y=-(x+3),\,\,\, -(-x)\le -2$
$\implies y= -x-3,\,\,\, -x \ge 2$
$\implies y= -x-3,\,\,\, x \le -2$
(ii) $y = -(-x-1),\,\,\, -(-x)\gt -2$
$\implies y = x+1,\,\,\, -x\lt 2$
$\implies y = x+1,\,\,\, x\gt -2$

For Part (c), my graph is correct, as per the solution given; as the solution shows the ordinate axis starting from $y=1$.
Part (c):
(i) $y = -(x+2)+3,\,\,\, x+2\le 2\implies y = -x+1,\,\,\, x\le 0$
(ii) $y = (x+2)-1,\,\,\, (x+2)\gt 2\implies y = x+1,\,\,\, x\gt 0$

For Part (d), my graph is correct, as per the solution given; as the solution shows the ordinate axis starting from $y=1$.
Part (d):
(i) $y = -2x+3,\,\,\, 2x\le 2\implies y = -2x+3,\,\,\, x\le 1$
(ii) $y = 2x-1,\,\,\, 2x\gt 2\implies y = 2x-1,\,\,\, x\gt 1$

For Part (e), the solution given is not clear about minimum value of function being $1$; hence unsure.
Part (e):
(i) $y = -(3x-6)+3= -3x+9,\,\,\, 3x-6\le 2\implies y = -3x+9,\,\,\, x\le 2\frac 23$
(ii) $y = 3x-7,\,\,\, 3x-6\gt 2\implies y = 3x-7,\,\,\, x\gt 2\frac 23$

Edit : Have found the correct solution in part (b) by only affecting the domain with change of $x$ by $-x$ to get equations:

Part (b):
(i) $y=-(x+3),\,\,\, (-x)\le 2$
$\implies y= -x-3,\,\,\, x \ge -2$
(ii) $y = -(-x-1),\,\,\, (-x)\gt 2$
$\implies y = x+1,\,\,\, x\lt -2$

But, seems like am missing theory as why for $g(x)=-f(-x)$ only the domain is affected by exchanging $x$ by $-x$; even though it means that the whole function is also negated.

jiten
  • 4,524
  • 2
    This problem can be solved by just sketching $f(x)$ and then shifting/scaling/mirroring the plot you made to get the other plots. 1) $f(x+a)$: this is a shift of the original graph by $-a$ in the $x$-direction. 2) $f(bx)$: this is the same as scaling the $x$-axis by $1/b$. If it's negative you must also mirror $f$ about the $y$-axis. 3) $f(bx+a)$ can be gotten by combining $1)$ and $2)$. 4) $af(x)$ scale the $y$-axis by $a$. If $a$ is negative mirror about the $x$-axis. – Winther Jun 22 '19 at 12:04
  • @Winther Agreed, & feel that the arithmetic approach can be derived from the graphical one. I.e, the if $f(x+a)$, then domain is affected by subtracting $a$ from the domain limits. Similarly, for $f(ax)$, the domain is modified by dividing by $a$. – jiten Jun 22 '19 at 17:06

2 Answers2

3

Perhaps you can think that the negative on the outside is changing the sign of the output, so that negative is not affecting the domain. Also, in general you can think that if $g(x) = -f(-x)$, then that means that the graph of $g$ is the result of flipping the graph of $f$ first over the $y$-axis (that is what the inside negative is doing) and then flipping the resulting graph over the $x$-axis (that is what the outside negative is doing).

enter image description here

Erin Carmody
  • 273
1

Most likely you were expected to sketch this out without such details by understanding what does each operation do. That is just do what the comments did.

part $(e)$ is fine.

\begin{align} f(x) &= \begin{cases} -x+3&, x\le 2 \\ x-1 &, x>2\end{cases} \end{align}

\begin{align} \color{red}-f(\color{blue}-x) &= \begin{cases} \color{red}-(-(\color{blue}-x)+3)&, \color{blue}-x\le 2 \\ \color{red}-(\color{blue}-x-1) &, \color{blue}-x>2\end{cases}\\ &=\begin{cases} -x-3&, x\ge -2 \\ x+1 &, x<-2\end{cases}\\ \end{align}

The negative outside just flip the graph about the $x$-axis, it doesn't affect the horizontal position.

Siong Thye Goh
  • 149,520
  • 20
  • 88
  • 149
  • Please help with my post on finding tangent's intercept for $y=\tan(2x)$ at: https://math.stackexchange.com/q/3270978/424260. – jiten Jun 22 '19 at 19:25
  • Please help with my previous comment's post - either there, or in chatroom at: https://chat.stackexchange.com/rooms/94404/discussion-between-siong-thye-goh-and-jiten. The issue there is that I want to see the problem from the angle of domain being provided by $(\frac{\pi}2,0)$; rather than seeing that as coordinate of intersection point of tangent to the curve $y=\tan(2x)$. My edit to the post highlights this issue, but seemingly is going unnoticed as took too much time (3 hours) to edit the post. – jiten Jun 23 '19 at 03:15
  • Please help with my post at: https://math.stackexchange.com/q/3276877/424260. It is concerned with a small finite geometric series. – jiten Jun 28 '19 at 09:21
  • Please help with my post at : https://math.stackexchange.com/q/3283651/424260. It is concerned with paradox of wheel's rim moving backward. – jiten Jul 05 '19 at 05:21
  • hmm i can't. i m not an expert in cycloid. also, i do not know what you are asking. – Siong Thye Goh Jul 06 '19 at 03:26
  • Although it is wrong to ask, but a detailed comment even would have helped me in thinking how the given answer fits in. In particular it refers mainly to the reverse motion of the rim point, and the other points above it. It would require desmos too. But, then chat would be better based on your response. – jiten Jul 08 '19 at 02:06
  • The best way to state that (i.e. what I want to ask) is to help me fill in the steps at : https://teacher.desmos.com/activitybuilder/custom/56041a19b223e5bb2da1a3fe. Also, this would help me understand desmos graph (by: http://www.math.montana.edu/malo/172f18/Thanksgiving-sol.pdf; as part of Q.6 on pg. 4) at: https://www.desmos.com/calculator/pcfjfrivo1. – jiten Jul 08 '19 at 12:17