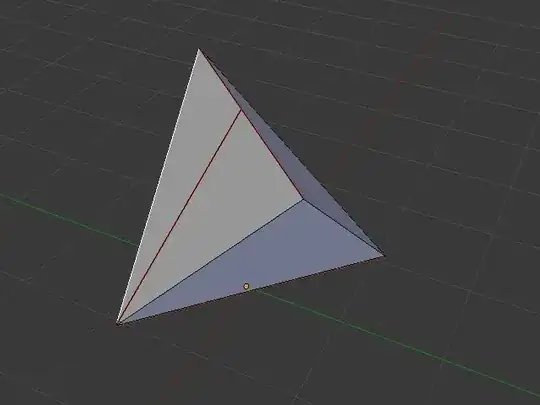
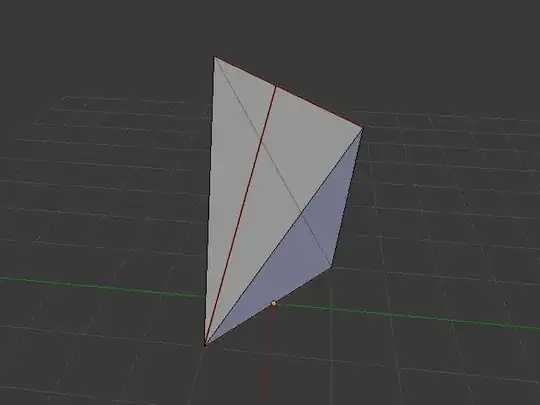
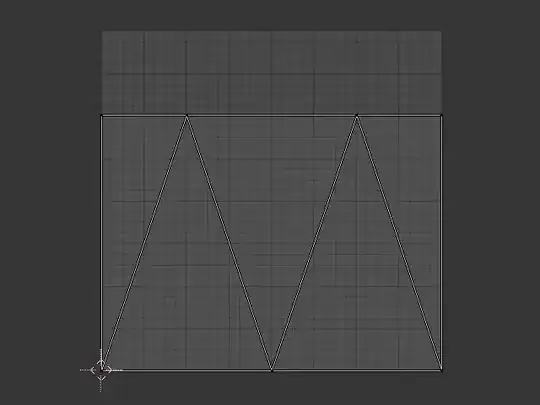
Is there a shape that can be wrapped perfectly?

Question

Wrapping presents in the real world always involves overlapping paper (due to folds, etc).

Is there any shape that can (theoretically) be wrapped by a rectangular piece of paper without any overlap (the shape and the paper have the same surface area)?

If such a thing exists, I imagine it would have to have angles to allow the paper to wrap to another side. I don't care if the shape is concave or convex. The shape must have a volume greater than 0

Such a shape can have at most two dimensions, anything else involves a corner around which you must form a good (either two sections overlap or the same section over itself). — Nij, May 13 '18 at 19:28
I'm pretty sure this shape can be. Depending on what you mean by "wrapped perfectly", you're likely to run into trouble with anything less exotic. — Micah, May 13 '18 at 19:37
Anyway, it's hard to answer this question in the negative without more detail about what you mean by "shape." For some value of "shape" the answer can be proven to be "no" using the Gauss-Bonnet theorem. — Qiaochu Yuan, May 13 '18 at 23:15
@Qiaochu I'm not very familiar with this branch of mathematics. I'm not sure what definitions are common for "shape". Do you have any terms I can Google? — Nathan Merrill, May 14 '18 at 00:09
@Quiaochu Yuan Could you please define the shape that cannot be wrapped? — Narasimham, Oct 22 '18 at 00:17

score 5 · Accepted Answer · answered May 14 '18 at 20:05

5

One solution is a regular tetrahedron. We can even generalize this to tetrahedrons constructed from regular ones where we just pull two oposing edges apart. The following pictures show a 3D models in blender. The red edges show where we cut the surface apart (called seams) and on the right side we see the unwrapped net of each model (done using UV-unwrapping, usually done for texturing objects). We need to cut one triangle in half in order to get a rectangle (otherwise we'd just get a parallelogram).

We can easily observe that this technique can be used for any side ratio of rectangles.

answered May 14 '18 at 20:05

flawr

16,533
5
41
66

2

Fun fact: U.S. dollar bills are almost-exactly the proportion needed to make perfect regular tetrahedra this way: ideally, we want $4:\sqrt{3} = 4\sqrt{3}:3 \approx 6.928:3$, while the bill is about $7.057:3$. Also, referencing your top-right diagram, performing the folds in sequence from bottom to top, flattening at each step, one creates a near-perfect equilateral triangle; the final corner can be tucked into a created pocket. (I tip waitstaff with such triangles.) I learned this from a math journal article that used the proportion approximation to declare "U.S. currency is irrational". :) – Blue May 14 '18 at 20:27
Haha, that is really cool:) Do all denominations have the same ratio? – flawr May 14 '18 at 20:35
Yes. All U.S. bills are the same size. According to Wikipedia's "United States dollar" entry, the current "small-sized note" ($6.14$ by $2.61$ inches) was introduced in 1928. Before that, "large-sized notes" ($7.42$ by $3.125$ inches) had proportion $7.12:3$, which are still probably good enough for manual tetrahedron-making. – Blue May 14 '18 at 20:44

Is there a shape that can be wrapped perfectly?

1 Answers1

Linked