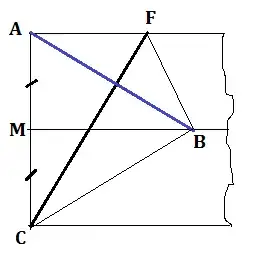
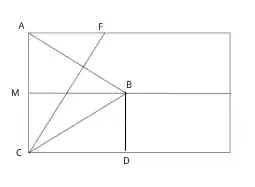
A rectangular strip of paper edge $AC$ is first folded in half making fold crease through mid-point $M$ and again bent folded along a new line through $C$ adjusted such that corner $A$ falls on divider $MB$. Show that triangle $ABC$ is equilateral.
EDIT1:
Rajendra Kumar makes a full Icosahedron repeated in this way!