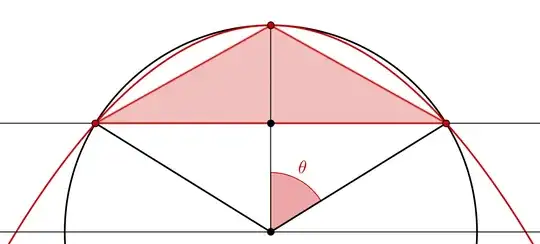
Here's a geometric argument, but it isn't as slick as some of the Calculus-based ones.
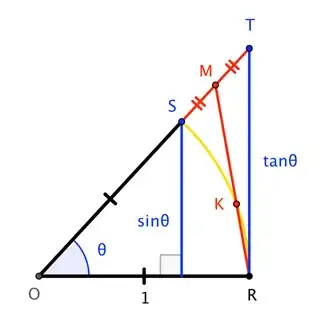
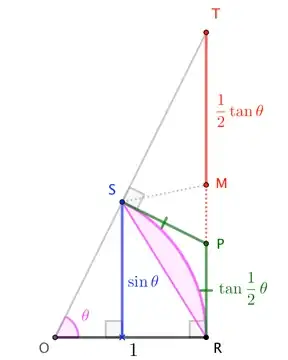
Consider the unit circle about $O$, through $R$ and $S$, with $\theta = \angle ROS$. The perpendicular from $S$ to $\overline{OR}$ has length $\sin\theta$, while the perpendicular from $R$ up to $T$ on the extension of $\overline{OS}$ has length $\tan\theta$. Let $M$ be the midpoint of $\overline{ST}$.
Then
$$2\;|\text{area of sector}\;ROS| = \theta \qquad\text{and}\qquad 2\;|\triangle ORM| = \frac{1}{2}\left(\sin\theta + \tan\theta\right)$$
"All we need to do" is show that the triangle has more area than the sector. This seems pretty clear; after all, the triangle contains almost-all of the sector, except for the circular segment defined by $\overline{KR}$, where $K$ is the intersection of $\overline{RM}$ and the circle. There is a concern, though, that the excess area in the triangular region $KSM$ could be less than that of the tiny sliver of a circular segment for small $\theta$; we need to dispel that concern.
There's probably a simpler route to this, but I coordinatized and, with the help of Mathematica, found
$$M = \left(\frac{1 + \cos\theta}{2}, \frac{\sin\theta (1 + \cos\theta)}{2 \cos\theta}\right)$$
$$K = \left(\frac{1 + 3 \cos\theta + 2 \cos^2\theta + 2 \cos^3\theta}{1 + 3 \cos\theta + 4 \cos^2\theta}, \frac{2 \sin\theta \cos\theta ( 1 + \cos\theta)}{1 + 3 \cos\theta + 4 \cos^2\theta}\right)$$
so that (after a bit more symbol-crunching)
$$\frac{|\overline{MK}|}{|\overline{KR}|} = \frac{1 + 3 \cos\theta}{4 \cos^2\theta} = 1 + \frac{1 + 3 \cos\theta - 4 \cos^2\theta}{4 \cos^2\theta} = 1 + \frac{(1-\cos\theta)(1 + 4 \cos\theta)}{4 \cos^2\theta} > 1$$
for $0 < \theta < \pi/2$.
This says that $\overline{MK}$ is longer than $\overline{KR}$, so that we could reflect $R$ in $K$ to get $R^\prime$, and copy circular segment $KR$ as circular segment $KR^\prime$ inside $\triangle ORM$ yet tangent to the unit circle (and therefore outside of sector $ORS$).
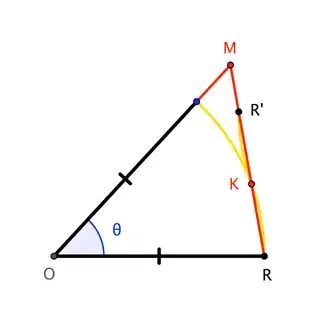
Consequently, the triangle definitely has more area than the sector, so we're done. $\square$