2

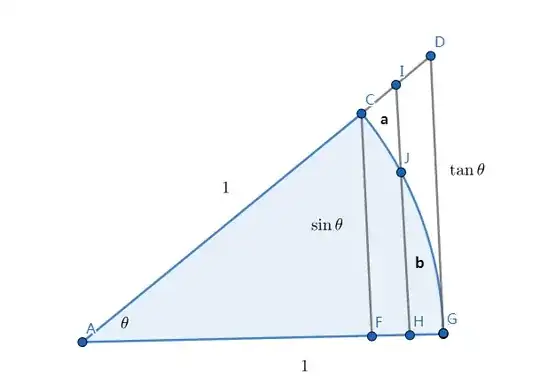
I could show in calculus where $0<θ<\frac{\pi}{2}$ like this

$$\frac{d(θ)}{dθ}=1<\frac{1}{2}(\cosθ+\sec^2θ)$$

But I curioused about would it could prove by geometric way likewise trigonometric identities. I try to show with the area of circular sector but I failed...

So this is question:

How to show $$\frac{\sinθ +\tanθ}{2}>\theta$$ where $0<\theta<\frac{\pi}{2}$ in geometric way?

StubbornAtom
  • 17,052
user366725
  • 751
  • Recall that $\theta$ is the length of the arc of radius $\theta$. This may be of help to prove the inequality geometrically on the unit circle – b00n heT Aug 23 '18 at 15:19
  • Please fix the geomatic/geomatric typos. –  Aug 23 '18 at 15:23
  • @YvesDaoust I fixed it – user366725 Aug 23 '18 at 15:25
  • 1
    @user366725: I am afraid not. –  Aug 23 '18 at 15:26
  • If you are interested in more calculus-based proofs, you can check Jack's and Martin's answer here: https://math.stackexchange.com/questions/2196624/prove-that-all-odd-derivate-of-tanx-at-x-0-is-at-least-1 – Botond Aug 23 '18 at 15:33
  • @Botond thanks~ – user366725 Aug 23 '18 at 15:36
  • @user366725 You can see a geometric approach to this problem in my answer here https://math.stackexchange.com/questions/2391978/is-there-a-geometrical-method-to-prove-x-frac-sin-x-tan-x2/2892328#2892328 – timon92 Aug 23 '18 at 16:50
  • @Joe: Using the full Taylor expansion would be incorrect. You need hard bounds otherwise all you can say is that the inequality holds in some open neighbourhood of the point. The hard bounds sufficient for this are $\sin(x) \ge x - x^3/6$ for every $x \ge 0$ and $\cos(x) \ge 1 - x^2/2$ for every $x \ge 0$. Both can be easily proven by repeated differentiation (and if you like to be rigorous, Rolle's theorem). Using these, you need to prove $(x - x^3/6)(4-x^2)/(2-x^2) \ge x$, which holds for $x \in [0,\sqrt{3}]$. – user21820 Aug 24 '18 at 03:40

1 Answers1

1

Here are some thoughts:

Approach $1a$

enter image description here

The blue region is a unit arc with an angle $\theta$. Let the length of $\overline {IH}$ be $\displaystyle L=\frac{\sin\theta+\tan\theta}2$.

The area of $\triangle AIH$ is given by $$S=\frac12 L\left(\frac L{\tan\theta}\right)=\frac{L^2}{2\tan\theta}\tag{1}$$

Notice the area of $\triangle ADG> \text{arc } ACG\implies\tan\theta>\theta\tag 2$

By $(1), (2)$

$$S<\frac{L^2}{2\theta}$$

Approach 1b

Notice arc $CJG$ has the length $\theta$. Then to prove $\theta<L$ is equivalent to prove the length of arc $CJG$ is shorter than the length of line $\overline {IH}$.

Mythomorphic
  • 6,008
  • To be honest, I don't think my attempt deserves to be an accepted answer. It is incomplete, plus it has a better and complete solution in the previous question. – Mythomorphic Aug 26 '18 at 16:07