1

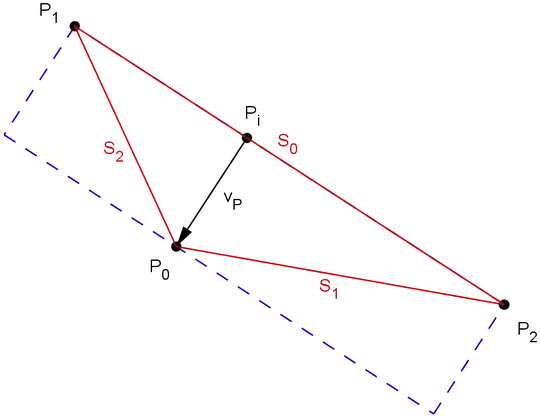
I am trying to transform a rectangle centered at the origin and dimensions of $(\| P_2 - P_1 \|, 0, \| \mathbf{V_P} \|)$ to a triangle in 3D space with points $P_0$, $P_1$, and $P_2$ where $\mathbf{V_P}$ is the vector perpendicular to the side shared by $P_1$ and $P_2$.

First, I will describe the information I currently know.

enter image description here

Points $P_1$ and $P_2$ are chosen such that their corresponding side, $S_0$, has the maximum length (in the case of an isosceles or equilateral triangle, any of the equal sides of maximum length may be chosen). Choosing this side to be the base ensures that the rectangle will share exactly one side with the triangle.

The coordinate system is right-handed with x to the right, y up, and -z forward.

Before translation, how can I rotate the original rectangle so that the resulting rectangle can be placed on top of the triangle such that the base of the rectangle lies on the maximum side of the triangle, $S_0$, like in the diagram?

I feel like my solution should be somewhat close to the answer in this question, using $x=(0, 1, 0)$ instead, but this does not quite work here.

Community
  • 1
Richard Voelker
  • 11

1 Answers1

0

After much research, trial and error, I have figured out the answer to my question.

I was right in thinking that the answer to this question was close to my answer; it is one step of the final solution. First, I find the normal vector of the final triangle:

$$ \hat n = Normalize((P_2 - P_1) \times (P_0 - P_1)) $$

We may then find the axis $\hat k$ and angle $\theta_k$ radians to rotate the rectangle so that the rectangle's normal, $\hat x = (0, 1, 0)$, becomes the triangle's normal, $\hat n$:

$$ \hat k = Normalize(\hat x \times \hat n)\\ \theta_k = cos^{-1}(\hat x \cdot \hat n) $$

The second and final step is to then get the base of the rectangle to match the base of the triangle. This can be done by rotating by $\theta_n$ radians around the normal vector $\hat n$. This can be found with the help of the right vector, $\hat r$, with respect to $\hat n$:

$$ \hat r = M_{AxisAngle(\hat k, \theta_k)} \cdot (1, 0, 0) $$

The angle $\theta_n$ is then the angle between $\hat r$ and the base of the triangle:

$$ \hat b = Normalize(P_2 - P_1)\\ \theta_n = cos^{-1}(\hat b \cdot \hat r) $$

This alone is not enough for a full answer, however. This angle is the shortest angle between the base vector, $\hat b$, and the right vector, $\hat r$ (i.e., $0 \le \theta_n \le \pi$).

Consider the triangle made up of three points around the origin:

$$ P_1^{'} = \hat b\\ P_2^{'} = -\hat b\\ P_r = \hat r $$

If the points of $\triangle P_1^{'}P_2^{'}P_r$ are in counter-clockwise order, then:

$$ \theta_n = cos^{-1}(\hat b \cdot \hat r) $$

Otherwise, if the points are in clockwise order:

$$ \theta_n = -cos^{-1}(\hat b \cdot \hat r) $$

To determine if the points are counter-clockwise, I use the answers posted in this other question. They are counter-clockwise if:

$$ ([\hat b - \hat r] \times [-\hat b - \hat r]) \cdot \hat n > 0 $$

The final rotation matrix, $M_R$, is then determined as follows:

$$ M_R = M_{AxisAngle(\hat n, \theta_n)} \cdot M_{AxisAngle(\hat k, \theta_k)} $$

Community
  • 1
Richard Voelker
  • 11