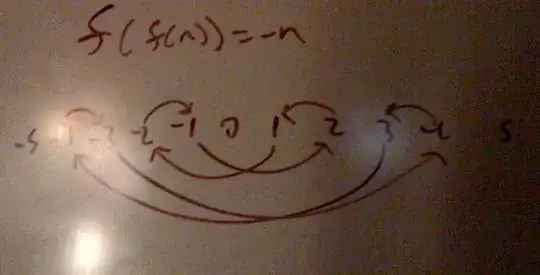A question I got on my last interview:
Design a function
f, such that:f(f(n)) == -nWhere
nis a 32 bit signed integer; you can't use complex numbers arithmetic.If you can't design such a function for the whole range of numbers, design it for the largest range possible.
Any ideas?
You didn't say what kind of language they expected... Here's a static solution (Haskell). It's basically messing with the 2 most significant bits:
f :: Int -> Int
f x | (testBit x 30 /= testBit x 31) = negate $ complementBit x 30
| otherwise = complementBit x 30
It's much easier in a dynamic language (Python). Just check if the argument is a number X and return a lambda that returns -X:
def f(x):
if isinstance(x,int):
return (lambda: -x)
else:
return x()
How about:
f(n) = sign(n) - (-1)ⁿ * n
In Python:
def f(n):
if n == 0: return 0
if n >= 0:
if n % 2 == 1:
return n + 1
else:
return -1 * (n - 1)
else:
if n % 2 == 1:
return n - 1
else:
return -1 * (n + 1)
Python automatically promotes integers to arbitrary length longs. In other languages the largest positive integer will overflow, so it will work for all integers except that one.
To make it work for real numbers you need to replace the n in (-1)ⁿ with { ceiling(n) if n>0; floor(n) if n<0 }.
In C# (works for any double, except in overflow situations):
static double F(double n)
{
if (n == 0) return 0;
if (n < 0)
return ((long)Math.Ceiling(n) % 2 == 0) ? (n + 1) : (-1 * (n - 1));
else
return ((long)Math.Floor(n) % 2 == 0) ? (n - 1) : (-1 * (n + 1));
}
Here's a proof of why such a function can't exist, for all numbers, if it doesn't use extra information(except 32bits of int):
We must have f(0) = 0. (Proof: Suppose f(0) = x. Then f(x) = f(f(0)) = -0 = 0. Now, -x = f(f(x)) = f(0) = x, which means that x = 0.)
Further, for any x and y, suppose f(x) = y. We want f(y) = -x then. And f(f(y)) = -y => f(-x) = -y. To summarize: if f(x) = y, then f(-x) = -y, and f(y) = -x, and f(-y) = x.
So, we need to divide all integers except 0 into sets of 4, but we have an odd number of such integers; not only that, if we remove the integer that doesn't have a positive counterpart, we still have 2(mod4) numbers.
If we remove the 2 maximal numbers left (by abs value), we can get the function:
int sign(int n)
{
if(n>0)
return 1;
else
return -1;
}
int f(int n)
{
if(n==0) return 0;
switch(abs(n)%2)
{
case 1:
return sign(n)*(abs(n)+1);
case 0:
return -sign(n)*(abs(n)-1);
}
}
Of course another option, is to not comply for 0, and get the 2 numbers we removed as a bonus. (But that's just a silly if.)
Thanks to overloading in C++:
double f(int var)
{
return double(var);
}
int f(double var)
{
return -int(var);
}
int main(){
int n(42);
std::cout<<f(f(n));
}
Or, you could abuse the preprocessor:
#define f(n) (f##n)
#define ff(n) -n
int main()
{
int n = -42;
cout << "f(f(" << n << ")) = " << f(f(n)) << endl;
}
This is true for all negative numbers.
f(n) = abs(n)
Because there is one more negative number than there are positive numbers for twos complement integers, f(n) = abs(n) is valid for one more case than f(n) = n > 0 ? -n : n solution that is the same same as f(n) = -abs(n). Got you by one ... :D
UPDATE
No, it is not valid for one case more as I just recognized by litb's comment ... abs(Int.Min) will just overflow ...
I thought about using mod 2 information, too, but concluded, it does not work ... to early. If done right, it will work for all numbers except Int.Min because this will overflow.
UPDATE
I played with it for a while, looking for a nice bit manipulation trick, but I could not find a nice one-liner, while the mod 2 solution fits in one.
f(n) = 2n(abs(n) % 2) - n + sgn(n)
In C#, this becomes the following:
public static Int32 f(Int32 n)
{
return 2 * n * (Math.Abs(n) % 2) - n + Math.Sign(n);
}
To get it working for all values, you have to replace Math.Abs() with (n > 0) ? +n : -n and include the calculation in an unchecked block. Then you get even Int.Min mapped to itself as unchecked negation does.
UPDATE
Inspired by another answer I am going to explain how the function works and how to construct such a function.
Lets start at the very beginning. The function f is repeatedly applied to a given value n yielding a sequence of values.
n => f(n) => f(f(n)) => f(f(f(n))) => f(f(f(f(n)))) => ...
The question demands f(f(n)) = -n, that is two successive applications of f negate the argument. Two further applications of f - four in total - negate the argument again yielding n again.
n => f(n) => -n => f(f(f(n))) => n => f(n) => ...
Now there is a obvious cycle of length four. Substituting x = f(n) and noting that the obtained equation f(f(f(n))) = f(f(x)) = -x holds, yields the following.
n => x => -n => -x => n => ...
So we get a cycle of length four with two numbers and the two numbers negated. If you imagine the cycle as a rectangle, negated values are located at opposite corners.
One of many solution to construct such a cycle is the following starting from n.
n => negate and subtract one -n - 1 = -(n + 1) => add one -n => negate and add one n + 1 => subtract one n
A concrete example is of such an cycle is +1 => -2 => -1 => +2 => +1. We are almost done. Noting that the constructed cycle contains an odd positive number, its even successor, and both numbers negate, we can easily partition the integers into many such cycles (2^32 is a multiple of four) and have found a function that satisfies the conditions.
But we have a problem with zero. The cycle must contain 0 => x => 0 because zero is negated to itself. And because the cycle states already 0 => x it follows 0 => x => 0 => x. This is only a cycle of length two and x is turned into itself after two applications, not into -x. Luckily there is one case that solves the problem. If X equals zero we obtain a cycle of length one containing only zero and we solved that problem concluding that zero is a fixed point of f.
Done? Almost. We have 2^32 numbers, zero is a fixed point leaving 2^32 - 1 numbers, and we must partition that number into cycles of four numbers. Bad that 2^32 - 1 is not a multiple of four - there will remain three numbers not in any cycle of length four.
I will explain the remaining part of the solution using the smaller set of 3 bit signed itegers ranging from -4 to +3. We are done with zero. We have one complete cycle +1 => -2 => -1 => +2 => +1. Now let us construct the cycle starting at +3.
+3 => -4 => -3 => +4 => +3
The problem that arises is that +4 is not representable as 3 bit integer. We would obtain +4 by negating -3 to +3 - what is still a valid 3 bit integer - but then adding one to +3 (binary 011) yields 100 binary. Interpreted as unsigned integer it is +4 but we have to interpret it as signed integer -4. So actually -4 for this example or Int.MinValue in the general case is a second fixed point of integer arithmetic negation - 0 and Int.MinValue are mapped to themselve. So the cycle is actually as follows.
+3 => -4 => -3 => -4 => -3
It is a cycle of length two and additionally +3 enters the cycle via -4. In consequence -4 is correctly mapped to itself after two function applications, +3 is correctly mapped to -3 after two function applications, but -3 is erroneously mapped to itself after two function applications.
So we constructed a function that works for all integers but one. Can we do better? No, we cannot. Why? We have to construct cycles of length four and are able to cover the whole integer range up to four values. The remaining values are the two fixed points 0 and Int.MinValue that must be mapped to themselves and two arbitrary integers x and -x that must be mapped to each other by two function applications.
To map x to -x and vice versa they must form a four cycle and they must be located at opposite corners of that cycle. In consequence 0 and Int.MinValue have to be at opposite corners, too. This will correctly map x and -x but swap the two fixed points 0 and Int.MinValue after two function applications and leave us with two failing inputs. So it is not possible to construct a function that works for all values, but we have one that works for all values except one and this is the best we can achieve.
Using complex numbers, you can effectively divide the task of negating a number into two steps:
The great thing is that you don't need any special handling code. Just multiplying by i does the job.
But you're not allowed to use complex numbers. So you have to somehow create your own imaginary axis, using part of your data range. Since you need exactly as much imaginary (intermediate) values as initial values, you are left with only half the data range.
I tried to visualize this on the following figure, assuming signed 8-bit data. You would have to scale this for 32-bit integers. The allowed range for initial n is -64 to +63. Here's what the function does for positive n:
For negative n, the function uses the intermediate range -65..-128.
Works except int.MaxValue and int.MinValue
public static int f(int x)
{
if (x == 0) return 0;
if ((x % 2) != 0)
return x * -1 + (-1 *x) / (Math.Abs(x));
else
return x - x / (Math.Abs(x));
}
The question doesn't say anything about what the input type and return value of the function f have to be (at least not the way you've presented it)...
...just that when n is a 32-bit integer then f(f(n)) = -n
So, how about something like
Int64 f(Int64 n)
{
return(n > Int32.MaxValue ?
-(n - 4L * Int32.MaxValue):
n + 4L * Int32.MaxValue);
}
If n is a 32-bit integer then the statement f(f(n)) == -n will be true.
Obviously, this approach could be extended to work for an even wider range of numbers...
for javascript (or other dynamically typed languages) you can have the function accept either an int or an object and return the other. i.e.
function f(n) {
if (n.passed) {
return -n.val;
} else {
return {val:n, passed:1};
}
}
giving
js> f(f(10))
-10
js> f(f(-10))
10
alternatively you could use overloading in a strongly typed language although that may break the rules ie
int f(long n) {
return n;
}
long f(int n) {
return -n;
}
Depending on your platform, some languages allow you to keep state in the function. VB.Net, for example:
Function f(ByVal n As Integer) As Integer
Static flag As Integer = -1
flag *= -1
Return n * flag
End Function
IIRC, C++ allowed this as well. I suspect they're looking for a different solution though.
Another idea is that since they didn't define the result of the first call to the function you could use odd/evenness to control whether to invert the sign:
int f(int n)
{
int sign = n>=0?1:-1;
if (abs(n)%2 == 0)
return ((abs(n)+1)*sign * -1;
else
return (abs(n)-1)*sign;
}
Add one to the magnitude of all even numbers, subtract one from the magnitude of all odd numbers. The result of two calls has the same magnitude, but the one call where it's even we swap the sign. There are some cases where this won't work (-1, max or min int), but it works a lot better than anything else suggested so far.
Exploiting JavaScript exceptions.
function f(n) {
try {
return n();
}
catch(e) {
return function() { return -n; };
}
}
f(f(0)) => 0
f(f(1)) => -1
For all 32-bit values (with the caveat that -0 is -2147483648)
int rotate(int x)
{
static const int split = INT_MAX / 2 + 1;
static const int negativeSplit = INT_MIN / 2 + 1;
if (x == INT_MAX)
return INT_MIN;
if (x == INT_MIN)
return x + 1;
if (x >= split)
return x + 1 - INT_MIN;
if (x >= 0)
return INT_MAX - x;
if (x >= negativeSplit)
return INT_MIN - x + 1;
return split -(negativeSplit - x);
}
You basically need to pair each -x => x => -x loop with a y => -y => y loop. So I paired up opposite sides of the split.
e.g. For 4 bit integers:
0 => 7 => -8 => -7 => 0
1 => 6 => -1 => -6 => 1
2 => 5 => -2 => -5 => 2
3 => 4 => -3 => -4 => 3
A C++ version, probably bending the rules somewhat but works for all numeric types (floats, ints, doubles) and even class types that overload the unary minus:
template <class T>
struct f_result
{
T value;
};
template <class T>
f_result <T> f (T n)
{
f_result <T> result = {n};
return result;
}
template <class T>
T f (f_result <T> n)
{
return -n.value;
}
void main (void)
{
int n = 45;
cout << "f(f(" << n << ")) = " << f(f(n)) << endl;
float p = 3.14f;
cout << "f(f(" << p << ")) = " << f(f(p)) << endl;
}
x86 asm (AT&T style):
; input %edi
; output %eax
; clobbered regs: %ecx, %edx
f:
testl %edi, %edi
je .zero
movl %edi, %eax
movl $1, %ecx
movl %edi, %edx
andl $1, %eax
addl %eax, %eax
subl %eax, %ecx
xorl %eax, %eax
testl %edi, %edi
setg %al
shrl $31, %edx
subl %edx, %eax
imull %ecx, %eax
subl %eax, %edi
movl %edi, %eax
imull %ecx, %eax
.zero:
xorl %eax, %eax
ret
Code checked, all possible 32bit integers passed, error with -2147483647 (underflow).
This Perl solution works for integers, floats, and strings.
sub f {
my $n = shift;
return ref($n) ? -$$n : \$n;
}
Try some test data.
print $_, ' ', f(f($_)), "\n" for -2, 0, 1, 1.1, -3.3, 'foo' '-bar';
Output:
-2 2
0 0
1 -1
1.1 -1.1
-3.3 3.3
foo -foo
-bar +bar
Uses globals...but so?
bool done = false
f(int n)
{
int out = n;
if(!done)
{
out = n * -1;
done = true;
}
return out;
}
Nobody ever said f(x) had to be the same type.
def f(x):
if type(x) == list:
return -x[0]
return [x]
f(2) => [2]
f(f(2)) => -2
Here is a solution that is inspired by the requirement or claim that complex numbers can not be used to solve this problem.
Multiplying by the square root of -1 is an idea, that only seems to fail because -1 does not have a square root over the integers. But playing around with a program like mathematica gives for example the equation
(18494364652+1) mod (232-3) = 0.
and this is almost as good as having a square root of -1. The result of the function needs to be a signed integer. Hence I'm going to use a modified modulo operation mods(x,n) that returns the integer y congruent to x modulo n that is closest to 0. Only very few programming languages have suc a modulo operation, but it can easily be defined. E.g. in python it is:
def mods(x, n):
y = x % n
if y > n/2: y-= n
return y
Using the equation above, the problem can now be solved as
def f(x):
return mods(x*1849436465, 2**32-3)
This satisfies f(f(x)) = -x for all integers in the range [-231-2, 231-2]. The results of f(x) are also in this range, but of course the computation would need 64-bit integers.
I'm not actually trying to give a solution to the problem itself, but do have a couple of comments, as the question states this problem was posed was part of a (job?) interview:
int.MinValue to int.MaxValue, and for each n in that range call f(f(n)) and checking the result is -n), telling I would then use Test Driven Development to get to such a function.Oh, this answer assumes the interview was for a C# programming related position. Would of course be a silly answer if the interview was for a math related position. ;-)
I would you change the 2 most significant bits.
00.... => 01.... => 10.....
01.... => 10.... => 11.....
10.... => 11.... => 00.....
11.... => 00.... => 01.....
As you can see, it's just an addition, leaving out the carried bit.
How did I got to the answer? My first thought was just a need for symmetry. 4 turns to get back where I started. At first I thought, that's 2bits Gray code. Then I thought actually standard binary is enough.
C# for a range of 2^32 - 1 numbers, all int32 numbers except (Int32.MinValue)
Func<int, int> f = n =>
n < 0
? (n & (1 << 30)) == (1 << 30) ? (n ^ (1 << 30)) : - (n | (1 << 30))
: (n & (1 << 30)) == (1 << 30) ? -(n ^ (1 << 30)) : (n | (1 << 30));
Console.WriteLine(f(f(Int32.MinValue + 1))); // -2147483648 + 1
for (int i = -3; i <= 3 ; i++)
Console.WriteLine(f(f(i)));
Console.WriteLine(f(f(Int32.MaxValue))); // 2147483647
prints:
2147483647
3
2
1
0
-1
-2
-3
-2147483647
Essentially the function has to divide the available range into cycles of size 4, with -n at the opposite end of n's cycle. However, 0 must be part of a cycle of size 1, because otherwise 0->x->0->x != -x. Because of 0 being alone, there must be 3 other values in our range (whose size is a multiple of 4) not in a proper cycle with 4 elements.
I chose these extra weird values to be MIN_INT, MAX_INT, and MIN_INT+1. Furthermore, MIN_INT+1 will map to MAX_INT correctly, but get stuck there and not map back. I think this is the best compromise, because it has the nice property of only the extreme values not working correctly. Also, it means it would work for all BigInts.
int f(int n):
if n == 0 or n == MIN_INT or n == MAX_INT: return n
return ((Math.abs(n) mod 2) * 2 - 1) * n + Math.sign(n)
Nobody said it had to be stateless.
int32 f(int32 x) {
static bool idempotent = false;
if (!idempotent) {
idempotent = true;
return -x;
} else {
return x;
}
}
Cheating, but not as much as a lot of the examples. Even more evil would be to peek up the stack to see if your caller's address is &f, but this is going to be more portable (although not thread safe... the thread-safe version would use TLS). Even more evil:
int32 f (int32 x) {
static int32 answer = -x;
return answer;
}
Of course, neither of these works too well for the case of MIN_INT32, but there is precious little you can do about that unless you are allowed to return a wider type.
I could imagine using the 31st bit as an imaginary (i) bit would be an approach that would support half the total range.
works for n= [0 .. 2^31-1]
int f(int n) {
if (n & (1 << 31)) // highest bit set?
return -(n & ~(1 << 31)); // return negative of original n
else
return n | (1 << 31); // return n with highest bit set
}
The problem states "32-bit signed integers" but doesn't specify whether they are twos-complement or ones-complement.
If you use ones-complement then all 2^32 values occur in cycles of length four - you don't need a special case for zero, and you also don't need conditionals.
In C:
int32_t f(int32_t x)
{
return (((x & 0xFFFFU) << 16) | ((x & 0xFFFF0000U) >> 16)) ^ 0xFFFFU;
}
This works by
After two passes we have the bitwise inverse of the original value. Which in ones-complement representation is equivalent to negation.
Examples:
Pass | x
-----+-------------------
0 | 00000001 (+1)
1 | 0001FFFF (+131071)
2 | FFFFFFFE (-1)
3 | FFFE0000 (-131071)
4 | 00000001 (+1)
Pass | x
-----+-------------------
0 | 00000000 (+0)
1 | 0000FFFF (+65535)
2 | FFFFFFFF (-0)
3 | FFFF0000 (-65535)
4 | 00000000 (+0)
:D
boolean inner = true;
int f(int input) {
if(inner) {
inner = false;
return input;
} else {
inner = true;
return -input;
}
}
return x ^ ((x%2) ? 1 : -INT_MAX);
I'd like to share my point of view on this interesting problem as a mathematician. I think I have the most efficient solution.
If I remember correctly, you negate a signed 32-bit integer by just flipping the first bit. For example, if n = 1001 1101 1110 1011 1110 0000 1110 1010, then -n = 0001 1101 1110 1011 1110 0000 1110 1010.
So how do we define a function f that takes a signed 32-bit integer and returns another signed 32-bit integer with the property that taking f twice is the same as flipping the first bit?
Let me rephrase the question without mentioning arithmetic concepts like integers.
How do we define a function f that takes a sequence of zeros and ones of length 32 and returns a sequence of zeros and ones of the same length, with the property that taking f twice is the same as flipping the first bit?
Observation: If you can answer the above question for 32 bit case, then you can also answer for 64 bit case, 100 bit case, etc. You just apply f to the first 32 bit.
Now if you can answer the question for 2 bit case, Voila!
And yes it turns out that changing the first 2 bits is enough.
Here's the pseudo-code
1. take n, which is a signed 32-bit integer.
2. swap the first bit and the second bit.
3. flip the first bit.
4. return the result.
Remark: The step 2 and the step 3 together can be summerised as (a,b) --> (-b, a). Looks familiar? That should remind you of the 90 degree rotation of the plane and the multiplication by the squar root of -1.
If I just presented the pseudo-code alone without the long prelude, it would seem like a rabbit out of the hat, I wanted to explain how I got the solution.
That's easy!
Example:
The rules are:
0 → 0
±2³¹ → ±2³¹
odd → even, even → -odd:
forall k, 0 < k < 2³⁰: (2k-1) → (2k) → (-2k+1) → (-2k) → (2k-1)
The only not matching values are ±(2³¹-1), because there are only two. There have to be two that cannot match, because there are only a multiple of four of numbers in a two's-complement system where 0 and ±2³¹ are already reserved.
In a one's complement system, there exist +0 and -0. There we go:
forall k, 0 < k < 2³⁰: (+2k) → (+2k+1) → (-2k) → (-2k-1) → (+2k)
In PHP
function f($n) {
if(is_int($n)) {
return (string)$n;
}
else {
return (int)$n * (-1);
}
}I'm sure you can understand the spirit of this method for other languages. I explicitly casted back to int to make it more clear for people who don't use weakly typed languages. You'd have to overload the function for some languages.
The neat thing about this solution is it works whether you start with a string or an integer, and doesn't visibly change anything when returning f(n).
In my opinion, the interviewer is asking, "does this candidate know how to flag data to be operated on later," and, "does this candidate know how to flag data while least altering it?" You can do this with doubles, strings, or any other data type you feel like casting.
Easy Python solution made possible by the fact that there were no restrictions on what f(x) was supposed to output, only f(f(x)):
def f(x):
return (isinstance(x, tuple) and -x[0]) or (x,)
I have another solution that works half of the time:
def f(x):
if random.randrange(0, 2):
return -x
return x
How about this?
int nasty(int input)
{
return input + INT_MAX/2;
}
Although the question said n had to be a 32 bit int, it did not say the parameter or return type had to be a 32 bit int. This should compile in java--in c you could get rid of the != 0
private final long MAGIC_BIT=1<<38;
long f(long n) {
return n & MAGIC_BIT != 0 ? -(n & !MAGIC_BIT) : n | MAGIC_BIT;
}
edit:
This actually makes for a really good interview question. The best ones are ones difficult or impossible to answer because it forces people to think it through and you can watch and look for:
etc.
Never just answer behavioral questions unless you have a VERY GOOD answer. Always be pleasant and try to involve the questioner. Don't get frustrated and don't give up early! If you really aren't getting anywhere, try something totally illegal that could work, you'll get nearly full credit.
Using the information given in the question, you can
So you basically go odd -> even -> odd or even -> odd -> even, and change the sign only for even numbers. The only number this does not work for is -2^31
Code:
function f(x) {
var neg = x < 0;
x = Math.abs(x) ^ 1;
if (x & 1) {
neg = !neg;
}
return neg ? -x : x;
}
This is also a solution (but we are bending the rules a little bit):
def f(n):
if isinstance(n,int):
return str(n)
else:
return -int(n)
I think the answer to these kind of questions are best explained visually by using diagrams. When we disregard zero, then we can partition the integers in small sets of 4 numbers:
1 → 2 3 → 4 5 → 6
↑ ↓ ↑ ↓ ↑ ↓ ...
-2 ← -1 -4 ← -3 -6 ← -5
This is pretty easy to translate to code. Note that even numbers change sign, and the odd numbers are increased or decreased by 1. In C# it would look like this:
public static int f(int x)
{
if(x == 0)
return 0;
if(x > 0)
return (x % 2 == 0) ? -x+1 : x+1;
// we know x is negative at this point
return (x % 2 == 0) ? -x-1 : x-1;
}
Of course you can shorten this method by using clever tricks, but I think this code explains itself best.
Then about the range. The 32-bit integers range from -2^31 upto 2^31-1. The numbers 2^31-1, -2^31-1 and -2^31 fall outside of the range of f(x) because the number 2^31 is missing.
#define STYPE int
STYPE sign_bit = (unsigned STYPE) 1 << ( sizeof ( STYPE ) * 8 - 1 );
STYPE f ( STYPE f )
{
unsigned STYPE smf = f > 0 ? f : -f | sign_bit;
smf += sign_bit >> 1;
return smf & sign_bit ? -( smf & ~sign_bit ) : smf;
}
Mine gives the right answer...50% of the time, all the time.
int f (int num) {
if (rand () / (double) RAND_MAX > 0.5)
return ~num + 1;
return num;
}
Here's a short Python answer:
def f(n):
m = -n if n % 2 == 0 else n
return m + sign(n)
General Case
A slight tweak to the above can handle the case where we want k self-calls to negate the input -- for example, if k = 3, this would mean g(g(g(n))) = -n:
def g(n):
if n % k: return n + sign(n)
return -n + (k - 1) * sign(n)
This works by leaving 0 in place and creating cycles of length 2 * k so that, within any cycle, n and -n are distance k apart. Specifically, each cycle looks like:
N * k + 1, N * k + 2, ... , N * k + (k - 1), - N * k - 1, ... , - N * k - (k - 1)
or, to make it easier to understand, here are example cycles with k = 3:
1, 2, 3, -1, -2, -3
4, 5, 6, -4, -5, -6
This set of cycles maximizes the ranges of inputs that will work within any machine type centered around zero, such as signed int32 or signed int64 types.
Analysis of compatible ranges
The map x -> f(x) in fact must form cycles of length 2 * k, where x = 0 is a special case 1-length cycle since -0 = 0. So the problem for general k is solvable if and only if the range of the input - 1 (to compensate for 0) is a multiple of 2 * k, and the positive and negative ranges are opposites.
For signed integer representations, we always have a smallest negative number with no positive counterpart in the range, so the problem becomes unsolveable on the complete range. For example, a signed char has range [-128, 127], so it's impossible for f(f(-128)) = 128 within the given range.
Lua:
function f(n)
if type(n) == "number" then
return (-number) .. ""
else
return number + 0
end
end
f(n) { return -1 * abs(n) }
How can I handle overflow problems with this? Or am I missing the point?
A bizarre and only slightly-clever solution in Scala using implicit conversions:
sealed trait IntWrapper {
val n: Int
}
case class First(n: Int) extends IntWrapper
case class Second(n: Int) extends IntWrapper
case class Last(n: Int) extends IntWrapper
implicit def int2wrapper(n: Int) = First(n)
implicit def wrapper2int(w: IntWrapper) = w.n
def f(n: IntWrapper) = n match {
case First(x) => Second(x)
case Second(x) => Last(-x)
}
I don't think that's quite the right idea though.
Clojure solution:
(defmacro f [n] (if (list? n) `(- ~n) n))
Works on positive and negative integers of any size, doubles, and ratios too!
Some were similar but just thought I would write down my first idea (in C++)
#include <vector>
vector<int>* f(int n)
{
returnVector = new vector<int>();
returnVector->push_back(n);
return returnVector;
}
int f(vector<int>* n) { return -(n->at(0)); }
Just using overloading to cause f(f(n)) to actually call two different functions
JavaScript one-liner:
function f(n) { return ((f.f = !f.f) * 2 - 1) * n; }
Another way is to keep the state in one bit and flip it with care about binary representation in case of negative numbers... Limit is 2^29
int ffn(int n) {
n = n ^ (1 << 30); //flip the bit
if (n>0)// if negative then there's a two's complement
{
if (n & (1<<30))
{
return n;
}
else
{
return -n;
}
}
else
{
if (n & (1<<30))
{
return -n;
}
else
{
return n;
}
}
}
number f( number n)
{
static count(0);
if(count > 0) return -n;
return n;
}
f(n) = n
f(f(n)) = f(n) = -n
int f(int n) {
return ((n>0)? -1 : 1) * abs(n);
}
How about this:
do
local function makeFunc()
local var
return function(x)
if x == true then
return -var
else
var = x
return true
end
end
end
f = makeFunc()
end
print(f(f(20000)))
Well, I am neither a math, nor a programming wizz, but isn't this pretty easy?
int f(int i) {
static bool b;
if (b) {
b = !b;
return i;
} else {
b = !b;
return -i;
}
}
Tested with big and small positive and negative values, INT_MIN, INT_MAX, it seems to work... Can be made thread safe if that is a concern, it wasn't a part of the assignment though.
Or maybe I am missing something?
C++
struct Value
{
int value;
Value(int v) : value(v) {}
operator int () { return -value; }
};
Value f(Value input)
{
return input;
}
Similar to the functions overload solution, in python:
def f(number):
if type(number) != type([]):
return [].append(number)
else:
return -1*number[0]
Alternative: static datamembers
Python 2.6:
f = lambda n: (n % 2 * n or -n) + (n > 0) - (n < 0)
I realize this adds nothing to the discussion, but I can't resist.
int f(int n)
{
static int x = 0;
result = -x;
x = n;
return result;
}
This is a one entry FIFO with negation. Of course it doesn't work for the max negative number.
Great question!
This took me about 35 secs to think about and write:
int f(int n){
static int originalN=0;
if (n!=0)
originalN=n;
return n-originalN;
}
Scala :
def f(x: Any): Any = x match {
case i: Int => new { override def hashCode = -i }
case i @ _ => i.hashCode
}
Same thing in Java :
public static Object f(final Object x) {
if(x instanceof Integer) {
return new Object() {
@Override
public int hashCode() {
return -(Integer)x;
}
};
}
return x.hashCode();
}
Another Javascript solution utilizing short-circuits.
function f(n) {return n.inv || {inv:-n}}
f(f(1)) => -1
f(f(-1)) => 1
Thought I'd try this one without looking at other people's answers first:
#include <stdio.h>
#include <limits.h>
#include <stdlib.h>
int f(int n) {
if(n > 0) {
if(n % 2)
return -(++n);
else {
return (--n);
}
}
else {
if(n % 2)
return -(--n);
else {
return (++n);
}
}
}
int main(int argc, char* argv[]) {
int n;
for(n = INT_MIN; n < INT_MAX; n++) {
int N = f(f(n));
if(N != -n) {
fprintf(stderr, "FAIL! %i != %i\n", N, -n);
}
}
n = INT_MAX;
int N = f(f(n));
if(N != -n) {
fprintf(stderr, "FAIL! n = %i\n", n);
}
return 0;
}
Output: [nothing]
Doesn't fail on MIN_INT:
int f(n) { return n < 0 ? -abs(n + 1) : -(abs(n) + 1); }
The problem as stated doesn't require that the function must ONLY accept 32 bit ints, only that n, as given, is a 32-bit int.
Ruby:
def f( n )
return 0 unless n != 0
( n == n.to_i ) ? 1.0 / n : -(n**-1).to_i
end
This will work in a very broad range of numbers:
static int f(int n)
{
int lastBit = int.MaxValue;
lastBit++;
int secondLastBit = lastBit >> 1;
int tuple = lastBit | secondLastBit;
if ((n & tuple) == tuple)
return n + lastBit;
if ((n & tuple) == 0)
return n + lastBit;
return -(n + lastBit);
}
My initial approach was to use the last bit as a check bit to know where we'd be in the first or the second call. Basically, I'd place this bit to 1 after the first call to signal the second call the first had already passed. But, this approach was defeated by negative numbers whose last bit already arrives at 1 during the first call.
The same theory applies to the second last bit for most negative numbers. But, what usually happens is that most of the times, the last and second last bits are the same. Either they are both 1 for negative numbers or they are both 0 for positive numbers.
So my final approach is to check whether they are either both 1 or both 0, meaning that for most cases this is the first call. If the last bit is different from the second last bit, then I assume we are at the second call, and simply re-invert the last bit. Obviously this doesn't work for very big numbers that use those two last bits. But, once again, it works for a very wide range of numbers.
Seems easy enough.
<script type="text/javascript">
function f(n){
if (typeof n === "string") {
return parseInt(n, 10)
}
return (-n).toString(10);
}
alert(f(f(1)));
</script>
Perhaps cheating? (python)
def f(n):
if isinstance(n, list):
return -n[0]
else:
return [n,0]
n = 4
print f(f(n))
--output--
-4
easy:
function f($n) {
if ($n%2 == 0) return ($n+1)*-1;
else return ($n-1);
}
In C,
int
f(int n) {
static int r = 0;
if (r == 1) {r--; return -1 * n; };
r++;
return n;
}
It would have helped to know what language this was for. Am I missing something? Many "solutions" seem overly complex, and quite frankly, don't work (as I read the problem).
Here's a C implementation of rossfabricant's answer. Note that since I stick with 32-bit integers at all times, f( f( 2147483647 ) ) == 2147483647, not -2147483647.
int32_t f( int32_t n )
{
if( n == 0 ) return 0;
switch( n & 0x80000001 ) {
case 0x00000000:
return -1 * ( n - 1 );
case 0x00000001:
return n + 1;
case 0x80000000:
return -1 * ( n + 1 );
default:
return n - 1;
}
}
If you define the problem to allow f() to accept and return int64_t, then 2147483647 is covered. Of course, the literals used in the switch statement would have to be changed.
how about this (C language):
int f(int n)
{
static int t = 1;
return (t = t ? 0 : 1) ? -n : n;
}
just tried it, and
f(f(1000))
returns -1000
f(f(-1000))
returns 1000
is that correct or am i missing the point?
Really, these questions are more about seeing the interviewer wrestle with the spec, and the design, error handling, boundary cases and the choice of suitable environment for the solution, etc, more than they are about the actual solution. However: :)
The function here is written around the closed 4 cycle idea. If the function f is only permitted to land only on signed 32bit integers, then the various solutions above will all work except for three of the input range numbers as others have pointed out. minint will never satisfy the functional equation, so we'll raise an exception if that is an input.
Here I am permitting my Python function to operate on and return either tuples or integers. The task spec admits this, it only specifies that two applications of the function should return an object equal to the original object if it is an int32. (I would be asking for more detail about the spec.)
This allows my orbits to be nice and symmetrical, and to cover all of the input integers (except minint). I originally envisaged the cycle to visit half integer values, but I didn't want to get tangled up with rounding errors. Hence the tuple representation. Which is a way of sneaking complex rotations in as tuples, without using the complex arithmetic machinery.
Note that no state needs to be preserved between invocations, but the caller does need to allow the return value to be either a tuple or an int.
def f(x) :
if isinstance(x, tuple) :
# return a number.
if x[0] != 0 :
raise ValueError # make sure the tuple is well formed.
else :
return ( -x[1] )
elif isinstance(x, int ) :
if x == int(-2**31 ):
# This value won't satisfy the functional relation in
# signed 2s complement 32 bit integers.
raise ValueError
else :
# send this integer to a tuple (representing ix)
return( (0,x) )
else :
# not an int or a tuple
raise TypeError
So applying f to 37 twice gives -37, and vice versa:
>>> x = 37
>>> x = f(x)
>>> x
(0, 37)
>>> x = f(x)
>>> x
-37
>>> x = f(x)
>>> x
(0, -37)
>>> x = f(x)
>>> x
37
Applying f twice to zero gives zero:
>>> x=0
>>> x = f(x)
>>> x
(0, 0)
>>> x = f(x)
>>> x
0
And we handle the one case for which the problem has no solution (in int32):
>>> x = int( -2**31 )
>>> x = f(x)
Traceback (most recent call last):
File "<pyshell#110>", line 1, in <module>
x = f(x)
File "<pyshell#33>", line 13, in f
raise ValueError
ValueError
If you think the function breaks the "no complex arithmetic" rule by mimicking the 90 degree rotations of multiplying by i, we can change that by distorting the rotations. Here the tuples represent half integers, not complex numbers. If you trace the orbits on a number line, you will get nonintersecting loops that satisfy the given functional relation.
f2: n -> (2 abs(n) +1, 2 sign( n) ) if n is int32, and not minint.
f2: (x, y) -> sign(y) * (x-1) /2 (provided y is \pm 2 and x is not more than 2maxint+1
Exercise: implement this f2 by modifying f. And there are other solutions, e.g. have the intermediate landing points be rational numbers other than half integers. There's a fraction module that might prove useful. You'll need a sign function.
This exercise has really nailed for me the delights of a dynamically typed language. I can't see a solution like this in C.
A C function:
int f(int n) /* Treats numbers in the range 0XC0000000 to 0X3FFFFFFF as valid to
generate f(f(x)) equal to -x. If n is within this range, it will
project n outside the range. If n is outside the range, it will
return the opposite of the number whose image is n. */
{
return n ? n > 0 ? n <= 0X3FFFFFFF ? 0X3FFFFFFF + n : 0X3FFFFFFF - n :\
n >= 0XC0000000 ? 0XC0000000 + n : 0XC0000000 - n : 0;
}
This one's in Python. Works for all negative values of n:
f = abs
Here's a variant I haven't seen people use. Since this is ruby, the 32-bit integer stuff sort of goes out the window (checks for that can of course be added).
def f(n)
case n
when Integer
proc { n * -1 }
when Proc
n.call
else
raise "Invalid input #{n.class} #{n.inspect}"
end
end
(-10..10).each { |num|
puts "#{num}: #{f(f(num))}"
}
One way to create many solutions is to notice that if we have a partition of the integers into two sets S and R s.t -S=S, -R=R, and a function g s.t g(R) = S
then we can create f as follows:
if x is in R then f(x) = g(x)
if x is in S then f(x) = -invg(x)
where invg(g(x))=x so invg is the inverse function for g.
The first solution mentioned above is the partition R=even numbers, R= odd numbers, g(x)=x+1.
We could take any two infinite sets T,P s.t T+U= the set of integers and take S=T+(-T), R=U+(-U).
Then -S=S and -R=R by their definitions and we can take g to be any 1-1 correspondence from S to R, which must exist since both sets are infinite and countable, will work.
So this will give us many solutions however not all of course could be programmed as they would not be finitely defined.
An example of one that can be is:
R= numbers divisible by 3 and S= numbers not divisible by 3.
Then we take g(6r) = 3r+1, g(6r+3) = 3r+2.
Easy, just make f return something that appears to equal any integer, and is convertable from an integer.
public class Agreeable
{
public static bool operator==(Agreeable c, int n)
{ return true; }
public static bool operator!=(Agreeable c, int n)
{ return false; }
public static implicit operator Agreeable(int n)
{ return new Agreeable(); }
}
class Program
{
public static Agreeable f(Agreeable c)
{ return c; }
static void Main(string[] args)
{
Debug.Assert(f(f(0)) == 0);
Debug.Assert(f(f(5)) == -5);
Debug.Assert(f(f(-5)) == 5);
Debug.Assert(f(f(int.MaxValue)) == -int.MaxValue);
}
}
const unsigned long Magic = 0x8000000;
unsigned long f(unsigned long n)
{
if(n > Magic )
{
return Magic - n;
}
return n + Magic;
}
0~2^31
What about following:
int f (int n)
{
static bool pass = false;
pass = !pass;
return pass? n : -n;
}
This will work for the range -1073741823 to 1073741822:
int F(int n)
{
if(n < 0)
{
if(n > -1073741824)
n = -1073741824 + n;
else n = -(n + 1073741824);
}
else
{
if(n < 1073741823)
n = 1073741823 + n;
else n = -(n - 1073741823);
}
return n;
}
It works by taking the available range of a 32 bit signed int and dividing it in two. The first iteration of the function places n outside of that range by itself. The second iteration checks if it is outside this range - if so then it puts it back within the range but makes it negative.
It is effectively a way of keeping an extra "bit" of info about the value n.
void f(int x)
{
Console.WriteLine(string.Format("f(f({0})) == -{0}",x));
}
Sorry guys... it was too tempting ;)
C++ solution;
long long f(int n){return static_cast <long long> (n);}
int f(long long n){return -static_cast <int> (n);}
int n = 777;
assert(f(f(n)) == -n);
Another cheating solution. We use a language that allows operator overloading. Then we have f(x) return something that has overloaded == to always return true. This seems compatible with the problem description, but obviously goes against the spirit of the puzzle.
Ruby example:
class Cheat
def ==(n)
true
end
end
def f(n)
Cheat.new
end
Which gives us:
>> f(f(1)) == -1
=> true
but also (not too surprising)
>> f(f(1)) == "hello world"
=> true
int f(const int n) {
static int last_n;
if (n == 0)
return 0;
else if (n == last_n)
return -n;
else
{
last_n = n;
return n;
}
}
Hackish, but correct.
int f(int n)
{
static long counter=0;
counter++;
if(counter%2==0)
return -n;
else
return n;
}
A Solution in SQL Server
create function dbo.fn_fo(@num int) -- OUTER FUNCTION
RETURNS int
AS
begin
RETURN @num * -1
end
GO
create function dbo.fn_fi(@num int) -- INNER FUNCTION
RETURNS int
AS
begin
RETURN @num * -1
end
GO
declare @num AS int = -42
SELECT dbo.fn_fo(dbo.fn_fi(@num)) -- Gives (-42)
perhaps I'm missing something?
Is this not something as simple as:
function f(n)
{
if(n ==0 || n < 0){return n;}
return n * -1;
}
Edit:
so I have miss read the question, ho-hum, so:
function f(n)
{
if(!c(n,"z")&&!c(n,"n")){if(n==0){return "z"+n;}return "n"+n;}
if( c(n,"z")){return 0;}return parseInt(n.replace("n",""))*-1;
}
function c(x,y){return x.indexOf(y) !==-1;}
ugly but works.
f(x) = the point (x) rotated 90 degrees counterclockwise around the origin in a 2D Cartesian coordinate system. Inputs of only one number x are presumed to be (x, 0), and outputs having y=0 are provided as the single number x.
object f: (object) x {
if (x.length == 1)
x = (x, 0)
swap = x[0]
x[1] = x[0]
x[0] = -swap
if (x[1] == 0)
x = x[0]
return x
I confess that I'd cheat, but meet the requirements nevertheless. This is programming wizardry, not really Mathematics. It works for the whole range, except -2^31.
int f(int n)
{
static bool eFlag = false; // Only executed once
eFlag = !eFlag;
return eFlag?-n:n;
}
Another cheating solution in C++, operator overloading.
struct func {
int n;
func operator()(int k) { n = -k; return *this; }
int operator()(const func &inst) { return inst.n; }
} f;
Objective-C
This works for all numbers except "-1".
If you are to go from using int to using NSInt then you can set -1 values to NULL and then convert them the second time to +1, but I feel that NSInt cheats what the asker intended.
f(n):
-(int)f:(int)n {
if (abs(n)==1) {
n = -1;
} else {
if (abs(n)%2) {//o
if (n>0) {//+
n--;
n*=+1;
} else if (n<0) {//-
n++;
n*=+1;
}
} else {//e
if (n>0) {//+
n++;
n*=-1;
} else if (n<0) {//-
n--;
n*=-1;
}
}
}
return n;
}
Of course this could all be shortened down to like one line, but then other people might not be able to read along...
Anyways, I stored the BOOLEAN logic in the state of the number being either odd or even.
I believe this meets all the requirements. Nothing says that the parameters have to be 32 bit signed integers, only that the value 'n' you pass in is.
long long f(long long n)
{
int high_int = n >> 32;
int low_int = n & 0xFFFFFFFF;
if (high_int == 0) {
return 0x100000000LL + low_int;
} else {
return -low_int;
}
}
let f n =
match n with
| n when n % 2 = 0 -> -n + System.Math.Sign n
| _ -> n - System.Math.Sign -n
where n such that System.Int32.MinValue < n < System.Int32.MaxValue.
I tried golfing this answer by Rodrick Chapman.
Without branches: 74 chars
int f(int i){return(-((i&1)<<1)|1)*i-(-((i>>>31)<<1)|1)*(((i|-i)>>31)&1);}
With branches, Java style: 58 chars
int f(int i){return i==0?0:(((i&1)==0?i:-i)+(i>0?-1:1));}
With branches, C style: 52 chars
int f(int i){return i?(((i&1)?-i:i)+(i>0?-1:1)):0;}
After a quick, but valid, benchmark, the branched version turns out to be 33% faster on my machine. (Random dataset of positive and negative numbers, enough repetition and prevented the compiler to optimize out the code, with warmup.) This is not so surprising, given the number of operations in the unbranched version and the possible good branch prediction because of the fact that the function is called twice: f(f(i)). When I change the benchmark to measure: f(i), the branched version is only 28% faster. I think this proves that the branch prediction actually did some good in the first case. More prove: when testing with f(f(f(f(i)))), it turns out the branched version is 42% faster.
Solution in the Wolfram Language:
f[f[n_]] := -n
Application:
In[2]:= f[f[10]]
Out[2]= -10
In[3]:= f[10]
Out[3]= f[10]
Because the question does not say anything the value of f(n), f[n] remains unevaluated.
C# overloading:
string f(int i) {
return i.ToString();
}
int f(string s) {
return Int32.Parse(s) * -1;
}
Or
object f(object o) {
if (o.ToString.StartsWith("s"))
return Int32.Parse(s.Substring(1)) * -1;
return "s" + i.ToString();
}
Tcl:
proc f {input} {
if { [string is integer $input] } {
return [list expr [list 0 - $input]]
} else {
return [eval $input]
}
}
% f [f 1]
-1
Along the lines of some of the other answers... if it's an integer, return a command that returns the negative of that number. If it's not a number, evaluate it and return the result.
This is a C/C++ solution that doesn't utilize any bitwise operators, and doesn't require any math libraries, though it's kind of cheating...
double f(double n)
{
if (n == (double)(int)n)
return n + 0.5;
else
return -(n - 0.5);
}
This works for all 32-bit integers with the single exception of 0x80000000 (since its opposite cannot be stored in the 32-bit integer system). f(f(n)) == -n will always be true except in that one case.
I'm sure there's a simpler and faster way to implement it, though. This was just the first thing that came to mind.
Javascript
function f(n) {
return typeof n === "number" ?
function() {return -n} :
n();
}
Based on the questions that Microsoft/Google's interviewers usually ask in their interviews, I believe the asker means an innovative, lightweight, simple solution that will use bitwise operations, not those complicated high level answers.
Inspired by the answer of @eipipuz, I wrote this C++ function (yet didn't run it):
int32_t f(int32_t n){
int32_t temp = n & 00111111111111111111111111111111;
x = n >> 30;
x++;
x = x << 30;
return x | temp;
}
It stores the leftmost two bits of n in x, adds 1 to x, and then replaces it as the leftmost two bits of n again.
If we keep running f(n) with another f(n) as the parameter n, the leftmost two bits will rotate like this:
00 --> 01 --> 10 --> 11 --> 00 ...
Note that the rightmost 30 bits don't change. Examples for 8 bit integers:
Example 1:
Example 2:
int func(int a)
{
static int p = 0;
int ret = a;
if ( p ) ret *= -1;
p ^= 1;
return ret;
}
I don't know if this is completely right, but wouldn't a simple flag work? In C, using a static local variable, I successfully did this:
int main()
{
int n = -256; // 32-bit signed integer
printf("%d", f(f(n)));
}
int f(int n){
static int x = 0; // not returning negative;
switch(x){
case 0:
x = 1;
return n;
break;
case 1:
x = 0;
return -n;
break;
default:
return -999;
break;
}
}
#include <cmath>
int f(int n)
{
static int count = 0;
return ::cos(M_PI * count++) * n;
}
In awk, since there's hardly any information being passed down, one has to resort to methods that allows state information being passed as part of the function return, without jeopardizing the usability of what's being passed down :
jot - -5 5 | mawk 'function _(__,___) {
return (__~(___=" ")) \
\
? substr("",sub("^[ ]?[+- ]*",\
substr(" -",__~__,index("_"___,___)-\
(__~"[-]")),__))\
(__~"[-]"?"":___)__\
: (+__<-__?___:(___)___)__
} BEGIN { CONVFMT=OFMT="%.17g"
} {
print "orig", +(__=$(__<__))<-__?__:" "__,
"f(n)....", _(__),_(_(__)),_(_(_(__))),
_(_(_(_(__)))), _(_(_(_(_(__)))))
}' |gcat -n | lgp3 5
1 orig -5 f(n).... -5 5 -5 5 -5
2 orig -4 f(n).... -4 4 -4 4 -4
3 orig -3 f(n).... -3 3 -3 3 -3
4 orig -2 f(n).... -2 2 -2 2 -2
5 orig -1 f(n).... -1 1 -1 1 -1
6 orig 0 f(n).... 0 -0 0 -0 0
7 orig 1 f(n).... 1 -1 1 -1 1
8 orig 2 f(n).... 2 -2 2 -2 2
9 orig 3 f(n).... 3 -3 3 -3 3
10 orig 4 f(n).... 4 -4 4 -4 4
11 orig 5 f(n).... 5 -5 5 -5 5
So the limit of this is that only integers or floating point values already in a string format that can be used without risking , since an extra ASCII space \040 is prepended as state information
The upside of this method is that
it's willing to provide you with "negative-zero",
for integers less than 2^53 in absolute value,
simply adding a plus sign,
i.e. +f(f(_))
to the function call itself would have implicit type-casting done on your behalf, and the resulting value will once again be numeric
for Big Integers, just substr() out any leading spaces
handle bigintegers with ease without risking loss of precision from being type-casted to a double-precision float
`
1 orig -99999999999999999999999999999999
f(n)....
-99999999999999999999999999999999
99999999999999999999999999999999
-99999999999999999999999999999999
99999999999999999999999999999999
-99999999999999999999999999999999
2 orig -1239999999999999999999999999999
f(n).... -1239999999999999999999999999999
1239999999999999999999999999999
-1239999999999999999999999999999
1239999999999999999999999999999
-1239999999999999999999999999999`
I'm late to this party and it's probably a graveyard now. But I have 2 contributions, inspired by viraptor's previous Python answer using lambda. A reader might think that solution is only viable in an untyped language, and that in a typed language it would require some explicit extra tagging.
But below is solution 1 in Haskell (I'm not a Haskell expert). It cheats a little, because technically, the two f's are two different implementations. (one f :: Int -> () -> Int, and the other f :: (() -> Int) -> Int)
{-# LANGUAGE MultiParamTypeClasses, FlexibleInstances, FunctionalDependencies #-}
module Main where
class Tran σ τ | σ -> τ where
tran :: σ -> τ
instance Tran Int (() -> Int) where
tran n = \_ -> (-n)
instance Tran (() -> Int) Int where
tran g = g ()
f :: Tran σ τ => σ -> τ
f = tran
main :: IO ()
main = do
print $ f (f (42 :: Int)) -- --> -42
print $ f (f (0 :: Int)) -- --> 0
print $ f (f (-69 :: Int)) -- --> 69
Next is solution 2 in Typed Racket. This one satisfies the property for the largest domain possible, because Number in Racket includes up to complex numbers:
#lang typed/racket
(: f (case->
[Number -> (-> Number)]
[(-> Number) -> Number]))
(define (f x)
(if (number? x) (λ () (- x)) (x)))
(f (f 42)) ; --> -42
(f (f 0)) ; --> 0
(f (f -69)) ; --> 69
(f (f 3/4)) ; --> -3/4
(f (f 8+7i)) ; --> -8-7i
This idea's been used in other answers, but I got it into one line of Python:
def f(n):
return str(n) if type(n) == int else -int(n)
using a cyclic permutation method to do this.
-b a b -a
a b -a -b
in the trivial situation f(0) returns 0
sorry for my rough answer by my phone, after 28th i will post a full version (now examing... ) briefly saying, think f(n) is a cyclic permutation,the questions is how to construct it.
define fk = f(f(f(f(...f(n))))) (k fs) situation k=2 0.trivial situation f(0) returns 0 1. make groups , in situation k=2, groups: {0} {1,2} {3,4} ... {n,n+1 | (n+1)%2 = 0 } ,attention: I ONLY use Z+, because the construction doesnt need use negative number. 2.construct permutation : if n % 2 = 0, so a=n-1 b=n if n % 2 = 1, so a=n b=n+1
this will generate the same permutation, because n and f(n) are in the same group.
note the permutation as P return P(n)
for k=2t , only doing the same things above, just MOD k. for k=2t-1, although the method works, but it makes no sense, ahh? (f(n) = -n is ok)
it's cheating by saving state but it works, break operation into two: -n = (~n + 1) for integers
int f(int n) {
static int a = 1;
a = !a;
if (a) {
return (~n);
} else {
return (n+1);
}
}
I thought the largest range possible was hinting at a modular arithmetic solution. In some modular bases M there is number which when squared is congruent to M-1 (which is congruent to -1). For example if M=13, 5*5=25, 25 mod 13=12 (= -1)
Anyway here's some python code for M=2**32-3.
def f(x):
m=2**32-3;
halfm=m//2;
i_mod_m=1849436465
if abs( x ) >halfm:
raise "too big"
if x<0:
x+=m
x=(i_mod_m*x) % m
if (x>halfm):
x-=m
return x;
Note there are 3 values it wont work for 2 ** 31-1, -(2 ** 31-1) and -(2 ** 31)
int f(int x){
if (x < 0)
return x;
return ~x+1; //two's complement
}
PHP, without using a global variable:
function f($num) {
static $mem;
$answer = $num-$mem;
if ($mem == 0) {
$mem = $num*2;
} else {
$mem = 0;
}
return $answer;
}
Works with integers, floats AND numeric strings!
just realized this does some unnecessary work, but, whatever
Isn't remembering your last state a good enough answer?
int f (int n)
{
//if count
static int count = 0;
if (count == 0)
{
count = 1;
return n;
}
if (n == 0)
return 0;
else if (n > 0)
{
count = 0;
return abs(n)*(-1);
}
else
{
count = 0;
return abs(n);
}
}
int main()
{
int n = 42;
std::cout << f(f(n))
}
I haven't looked at the other answers yet, I assume the bitwise techniques have been thoroughly discussed.
I thought I'd come up with something evil in C++ that is hopefully not a dupe:
struct ImplicitlyConvertibleToInt
{
operator int () const { return 0; }
};
int f(const ImplicitlyConvertibleToInt &) { return 0; }
ImplicitlyConvertibleToInt f(int & n)
{
n = 0; // The problem specification didn't say n was const
return ImplicitlyConvertibleToInt();
}
The whole ImplicitlyConvertibleToInt type and overload is necessary because temporaries can't be bound to a non-const reference.
Of course, looking at it now it's undefined whether f(n) is executed before -n.
Perhaps a better solution with this degree of evil is simply:
struct ComparesTrueToInt
{
ComparesTrueToInt(int) { } // implicit construction from int
};
bool operator == (ComparesTrueToInt, int) const { return true; }
ComparesTrueToInt f(ComparesTrueToInt ct) { return ComparesTrueToInt(); }
int f(int n) { return (n <= 0) ? n : f(-n); }
static int f(int n) {
if (n <= 0)
return n;
else
return f(-n);
}
static void Main(string[] args) {
for (int n = int.MinValue; n < int.MaxValue; n+=1) {
Console.Out.WriteLine("Value: " + n + " Result: " + f(f(n)));
}
}
And it works ( assuming I understand the question properly )
How about
int f(int n)
{
return -abs(n);
}
