For a GPS receiver to estimate its position, it first receives signals from at least 4 satellites. Does the receiver calculate the distance that separates it from each satellite, or does it just calculate the distance difference between each pair of satellites?
In other words, does the GPS system use TOF (time of flight) or TDOA (time difference of arrival, aka multilateration) technique to calculate position and how are these techniques applied?
Does the receiver calculate the distance that separates it from each satellite, or does it just calculate the distance difference between each pair of satellites?
A basic answer is a global navigation satellite system (GNSS) computes satellite distance using the time of departure inserted by the satellite in the GNSS navigation message, and the time of arrival (TOA) measured with the receiver clock.
Such distance is approximate, called a pseudorange: Satellite and receiver clocks have no easy mean to be synchronized and they don't indicate the same time. So the travel time is biased by a systematic error.
Because the bias is the same for all measurements, it can be computed as a 4th unknown in addition of X, Y and Z, and actual ranges found, by using a 4th pseudorange from a 4th satellite and building a system of 4 equations.
Stolen at psu.edu.
In other words, does the GPS system use TOF (time of flight) or TDOA (time difference of arrival, aka multilateration) technique to calculate position.
GNSS uses a trilateration technique to determine pseudoranges, based on TOF.
At least this is how the US GPS was designed. And this is how most GNSS receivers work. The receiver doesn't requires precision elements, and position determination is very fast.
But it is possible to determine a position using TDOA techniques, a lot more precise though either more expensive or with more constraints, in particular they may be dependent on multiple receivers. They are not based on transit times, but on carrier phase observation.
Details for both methods follow.
Usual method: Travel time and pseudorange
GNSS signal consists in the navigation message bitstream transmitted at a rate of 50 bits per second on the main GNSS carrier L1, which frequency is around 1,500 MHz. The total transmission time is 12.5 minutes. This message contains:
Orbital elements of the satellite (ephemeris) which when combined with a time give a precise satellite position.
Constellation almanac, a reduced ephemeris version for all satellites in the GNSS constellation. So the receiver knows which satellites are in sight at a given time, and approximately where, this prevents searching for satellites which are not accessible.
Telemetry data (TML), including the time each subframe of the navigation message was sent. A subframe is a 6-second message chunk.
To determine the time of arrival of a repeating and continuous signal, the receiver must first identify specific marks in the bitstream: Bit edges occurring when a bit switches from 0 to 1 or from 1 to 0.
At 50 bps, edges are not close enough in time to allow a precise receiver synchronization. This rate is therefore increased by chipping the original bits with a faster repeating bits sequence, and sending the result in place of the original. The chipping bits must be recreated by the receiver in order to rebuild the original bits of the navigation message.
There are two chipping sequences, one publicly available, the coarse acquisition code (C/A), and one accessible only to authorized users, the precise P code which can be encrypted under the name of Y code, so this sequence is often referred to as P(Y).
C/A and P sequences are particular to a satellite. Each satellite is given an ID which is used to seed a pseudorandom noise (PRN) generator to create custom C/A and P sequences.
We may wonder the reason we introduce individual sequences and why they are random:
All satellites share the same carrier L1, but receivers must be able to synchronize on a particular satellite and ignore the other. Different PRN sequences facilitate this extraction.
A random sequence produces a final L1 signal with a homogeneously spread spectrum (frequencies distribution around the carrier). As the spectrum is also dependent on the PRN sequence, satellites in the constellation have non-overlapping spectrums, and interferences are prevented (see spread spectrum for a detailed presentation).
The difference between C/A and P codes is how much bits are used to chip a single bit (20 ms) of the navigation message. The chipping frequency, by creating more or less timing edges (phase shifts) in the modulated signal has a direct influence on the ranging precision, as well on the width of the spread spectrum.
The C/A sequence is 1023 bits long sequence repeating each ms. A bit is therefore sliced into 20,460 smaller bits:
When flowing at c speed, this smaller bit occupies 300 m in space. A receiver is assumed to be able to synchronize on edges with a precision of 1% of the distance between edges, so 3 m in optimum conditions.
P code bits are 10 times shorter than C/A bits, each occupying 3 m in space, allowing a better precision of 30 cm.
The receiver knows the ID (PRN) of the satellites in sight, from an almanac previously collected and stored. It generates the C/A code and look for corresponding changes in L1 signal. If found, the datastream is decoded to get the navigation messageg. Departures times are found in the decoded navigation message, in telemetry data, and compared with the local time.
To generate a P code, in addition of the public PRN, the pseudorandom generator also needs a second seed, delivered to authorized users only. If the receiver is provided this seed it can repeat the process and obtain a better estimate of the TOA by decoding the P-encoded stream, also present in the signal, phase-shifted by 90° to prevent mixing.
Alternate method: Phase observation
Traveling time is one observable of GNSS signal, the other is the carrier phase. With phase, no codes are required (tough a P code pseudorange is usually computed to speed up the solution). These methods look at the carrier wave.
Say we observe L1 carrier, which on the GPS is 1575 MHz frequency, a wavelength of about 20 cm. If we can count the cycles + the fraction of cycle present between the transmitter and the receiver, and knowing the frequency, we have measured the total path length, so the range.
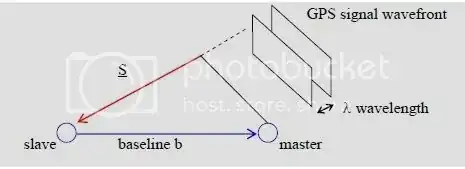
We cannot count all the cycles, but we can count the portion close to the ground. One method is to set two receivers, and count the cycles this way:
We want to know the number of cycles from the first receiver to the point which belongs to the carrier wavefront received by the second receiver. From this it is possible to derive the distance to the satellite.
The portion of wave to measure is made of a full number of cycles, and a factional part. The fractional part is the easiest to determine. what is a challenge is to know the integer number of cycles. This is the integer ambiguity resolution problem. Several techniques exists, some take hours of measurement, some are real time (e.g. RTK which is a commercial product).
Such phase observation techniques are not pseudorange determination, nor in the TOA category. They are based on the observation of the carrier phase, and are quite similar to interferometry.
As soon as the signal frequency is known, phase and time are interchangeable, a phase difference of $2 \pi$ rad is equal to $1/f$ s. What we measure is the difference in time of arrival at two different stations.
I think GPS receivers do not exclusively need at least 4 satellites, but rather 3 as a minimum for trilateration.
A fourth satellite signal is necessary to synchronize the receiver clock with the satellite clocks.
As for TOF/TOA vs. TDOA, I believe the difference relies whether on if the GPS receiver has an internal clock synchronized with the satellite transmitters or not. In other words, whether if you know the time on the satellite or not (in which case, you measure the range differences).
So, user-end GPS systems probably use TDOA as they wouldn't have a synchronized clock (would be too expensive).
Details on the GPS positioning calculations:
The GPS calculation in the receiver uses four equations in the four unknowns x, y, z, tc, where x, y, z are the receiver's coordinates, and tc is the time correction for the GPS receiver's clock.
The equation is:
\begin{equation} \ d_n = c(t_{t,n} - t_{r,n} + t_c) = \sqrt[]{(x_n-x)^2+(y_n-y)^2+(z_n-z)^2} \end{equation}
Where:
TOA = Time of arrival, TOF = Time of flight, TDOA = Time differences of arrival
Sources:
https://www.courses.psu.edu/aersp/aersp055_r81/satellites/gps_details.html
http://www.adv-radio-sci.net/9/203/2011/ars-9-203-2011.pdf
https://www.maa.org/sites/default/files/pdf/upload_library/22/Polya/Kalman.pdf
Thanks to @mins for an excellent answer.
This answer is “nice to know GPS trivia” which does not apply to current GPS devices.
It is possible to get a running fix from a single GPS satellite. In the early 1980’s, when there were only 4 operational GPS satellites, I was working on a hydrographic survey ship in the North Atlantic and Labrador Sea off of Greenland.
We would use the new-fangled GPS system to calibrate the shore-based DECCA radio-navigation system. DECCA would interpolate between GPS fixes.
There was never more than one satellite above the horizon, so a “running fix” strategy was used. The single GPS signal would give a time-of-flight range and therefore a “sphere of position”. Where this sphere of position intersected the surface of the Earth would give a “circle of position”. However, the Earth is not a sphere. The exact shape of the Earth (the “geoid”) was actually Top Secret during the cold war since it affected the path of ICBMs. The ship was working in collaboration with the US military, so we had access to their best data on the geoid as well as un-degraded signal processing from the GPS satellites.
The (roughly circular) circle of position would change as the GPS satellite followed its ground track shown in green in the sketch below:
The two points X and X’ are candidate fixes consistent with the satellite data. Of course, the ship was moving as the ground track progressed. And the Earth was rotating as well. Both these motions needed to be accounted for.
The computer would then twiddle its thumbs until another satellite (sometimes the same satellite) came over the horizon and repeat the process. Eventually the computer had enough information to provide a 3D fix. After correcting for changes in tidal height, the fix could be fed back to correct errors in the geoid database.
I don’t know the accuracy of these single-satellite fixes due to all the Cold War secrecy.”If I tell you, I’ll have to kill you.” But I believe the 3D fixes were in the order of a few meters since they needed to be corrected for the location of the GPS antennae on the bridge and the height of the bridge off the waterline. Even the ship’s heading needed to be fed to the computer since that affected the displacement direction of the antennae from the ship’s center.
Fortunately, things have got simpler.
GPS satellites can be used to determine the attitude of other satellites also. I am not an expert in this field, but it might work the same way for tracking of people/cars on Earth.
Anyway, this is how it works for satellites.
GPS sensors can be used to determine attitude provided that at least 3 antennas are vailable. The 4th is needed for timing.
Slave and master are 2 antennas mounted on the s/c. If the distance $b$ is known we can detect the s/c orientation in space. Taking the projection of $\underline{b}$ on the direction $\underline{S}$ of the incoming GPS signal we obtain the path difference of the signal received by the 2 antennas as $\underline{S}^T \underline{b}$.
The position of the GPS satellite is known, therefore $\underline{S}$ is known in the geocentric reference frame if we know the position of the master antenna.
Measuring the path difference
$\Delta r = \underline{S}^T \underline{b}$
and transforming the vector $\underline{S}$ from geocentric to body frame
$\underline{S} = AS$
$\Delta r = S^T A^T \underline{b} $
the unknown is the rotation matrix A.
Having 3 independent measurements:
$\Delta r_{11} = S_1^T A^T \underline{b}_1 $ baseline 1 GPS satellite 1
$\Delta r_{21} = S_2^T A^T \underline{b}_1 $ baseline 1 GPS satellite 2
$\Delta r_{12} = S_1^T A^T \underline{b}_2 $ baseline 2 GPS satellite 1
$\Delta r_{22} = S_2^T A^T \underline{b}_2 $ baseline 2 GPS satellite 2
...
2 baselines are required, otherwise if you have a single baseline you cannot determine the rotation around that baseline.
To determine attitude minimize the cost function:
$J = \sum_{i = 1}^{N_S} \sum_{j = 1}^{N_b} (\Delta r_{ij} - S_i^T A^T b_j)$
