What's the motion of two connected satellites orbiting the Earth after their separation?

Question

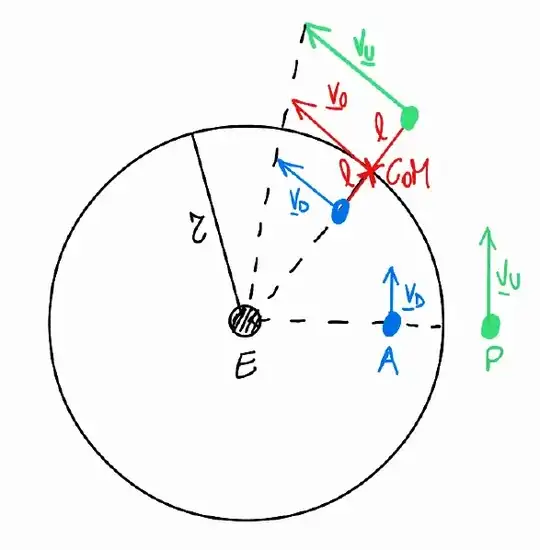
Let's consider the following problem (it's a job interview question): two satellites are orbiting the Earth in a circular orbit; they are rigidly linked by a tether which is always pointing in the radial direction. What happens as soon as the tether is cut?

Here is my reasoning:

Before cutting the tether the velocity of two satellites is equal to the one of the system CoM (Center of Mass); if we assume Keplerian Mechanics, from the specific mechanical energy equation we can derive the expression of the velocity magnitude,

$$ V_0 = V_U = V_D = \sqrt{ \frac{\mu}{r}} $$

After the tether is cut, we notice that the satellites are at different altitudes but we also know that the velocity and position vectors are perpendicular, hence the two satellites have to be on the apse lines of their orbits. The satellite at higher altitude is at the apogee of its orbit, since its kinetic energy is decreased with respect to the situation before cut, instead the satellite at lower altitude is at the perigee of its orbit since its kinetic energy is increased.

Is my reasoning correct? Can one add further considerations on the two orbits?

Answer 1

Many good things here, though a few of the assumptions made are not safe.

Before cutting the tether the velocity of two satellites is equal to the one of the system CoM

This can not be assumed. Gravity acting upon a mass that isn't spherically symmetric (which this, being two points, isn't) does not act as if upon a point mass at the centre of mass. Consider for instance what happens if your $\mathcal{l}$ is almost as large as $r$. The gravitational force on the lower satellite grows almost infinitely big, while the counteracting force of the upper tether must be some much smaller finite number.

Instead, consider that the forces acting in a co-rotating frame of reference must be balanced in order for the orbit to be circular:

$$\frac{\mu m_1}{r_1^2} + \frac{\mu m_2}{r_2^2} = m_1 \cdot \omega^2r_1 + m_2 \cdot \omega^2r_2$$

With $r_1$ and $r_2$ being $r\pm l$, this can be rearranged to get the angular velocity

$$\omega = \sqrt{\frac{\mu m_1/(r - l)^2 + \mu m_2/(r + l)^2}{m_1(r - l) + m_2(r + l)}}$$

---

$V_0 = V_U = V_D$

This can't be the case. If the tether stays radial, the lower satellite is orbiting in a smaller circle than the upper satellite with the same period, and must therefore move slower. The angular velocity on the other hand is equal:

$\omega_0 = \omega_U = \omega_D$

---

It is true that the satellites must be at their apsis points after the tether is cut, for the reason you state, but the periapsis and apoapsis are the other way around.

The lower satellite is in the original state orbiting slower than it "should" in free fall, with tension in the tether preventing it from losing altitude. Similarly, the upper satellite is orbiting "too fast" compared to a circular orbit of the same radius. When the tether is cut there is no change in kinetic energy, the satellites continuing with the same velocity as they already have. Thus, the inner satellite is now at its apoapsis, having no tether to keep the altitude, and the upper satellite is at its periapsis.

The upper satellite quite readily get on a hyperbolic trajectory.

Answer 2

Before the tether is cut, the angular velocity of the satellite is given by $$ \frac{\mu m_1}{r_1^2} + \frac{\mu m_2}{r_2^2} = m_1 \Omega^2 r_1 + m_2 \Omega^2 r_2 = M R \Omega^2, $$ where $r_1 = R - m_2 l / M$, $r_2 = R + m_1 l / M$, $R$ is the position of the center of mass, and $M = m_1 + m_2$. This then implies that $$ \Omega^2 = \frac{\mu}{M R} \left(\frac{m_1}{r_1^2} + \frac{m_2}{r_2^2} \right) = \frac{\mu}{R^3} \left( \frac{m_1/M}{(1 - m_2 l/R)^2} + \frac{m_2/M}{(1 + m_1 l/R)^2} \right) $$ In the case where the tether length is much shorter than the radius of the orbit (which seems like a physically reasonable assumption), this means that $$ \Omega^2 \approx \frac{\mu}{R^3} \left( 1 + \frac{3 m_r l^2}{M R^2} \right), $$ where $m_r = m_1 m_2/M$ is the reduced mass of the two satellites. In the case of $m_1 = m_2$ (which I'll be considering from now on for simplicity), we have $m_r = m_1/2$ and so $m_r/M = \frac14$.

If we now consider the motion in a reference frame rotating with the center of mass, the motion of each satellite after the separation will be given by $$ m_i \ddot{\vec{r}} = \vec{F}_g + m_i \Omega^2 r \hat{r} + 2 m_i \Omega \vec{v} \times \hat{z} $$ and writing this out in polar coordinates we get \begin{align} \ddot{r} - r \dot{\theta}^2 &= r \left( \Omega^2 - \frac{\mu}{r^3} + 2 \Omega \dot{\theta} \right) \\ r \ddot{\theta} + 2 \dot{r} \dot{\theta} &= - 2 \Omega \dot{r}. \end{align} If we now look for a perturbational solution where $r(t) = R(1 + \epsilon x(t))$ and $\theta(t) = \epsilon y(t)$ (with the small parameter $\epsilon = l/R$), then to $\mathcal{O}(\epsilon)$ we have $\Omega^2 R^3 = \mu$ and this all this reduces to $$ R \ddot{x} = 3 \Omega^2 R x + 2 R \Omega \dot{y} \qquad R \ddot{y} = - 2 R \Omega \dot{x} $$ Via standard techniques (i.e., whacking it into Mathematica) this can be solved for the initial conditions $x(0) = \pm \frac{1}{2} $ and $\dot{x}(0) = y(0) = \dot{y}(0) = 0$, with the result that $$ x(t) = \pm ( 2 - \frac{3}{2} \cos (\Omega t)) \qquad y = \pm (3 \sin (\Omega t) - 3 \Omega t) $$

So to interpret this: to first order in $l/R$,

• The satellites now oscillate between radii of $R \pm \frac{1}{2} l$ and $R \pm \frac{7}{2} l$, with an oscillation period equal to the orbital period before the tether was severed. The upper satellite will be at apogee at the same time the lower satellite is at perigee.
• The semimajor axes of the new orbits are (to this order) $a_\pm = R \pm 2l$. From Kepler's Third Law ($T \propto a^{3/2}$), this then implies that the new periods $T_\pm$ are related to the old period $T$ by $$T_\pm = T\left( 1 \pm 3 \frac{l}{R} \right).$$
• For each orbital period of the center of mass, the upper satellite will end up "behind" the center of mass by an angle of $6 \pi l/R$, and the lower satellite will end up "ahead" of the center of mass by an angle of $6 \pi l/R$.

A diagram of the situation in this regime is shown below. The blue dashed line is the circular orbit of the original satellite; the yellow and green curves are the satellites' subsequent orbits.