Why do we not fly to space with helicopters? What are the practical altitude limits?

Question

People will tell that there is no air, and this is why we cannot. But if I read on the internet, there is air in space, much less, but still something.

For example:

• 100 km: $6\ \cdot 10^{-7}$ times as much air as on the surface;
• 1000 km: $2.5\ \cdot 10^{-14}$ times as much air as on the surface;
• even on 36000 km there is something ($1.5\ \cdot 10^{-18}$ times as much air as on the surface or 30000 atoms per 1 cubic decimeter).

Talking practically: NASA already built a prototype of the helicopter which will fly on Mars where the atmosphere is the same as 30 km high on The Earth.

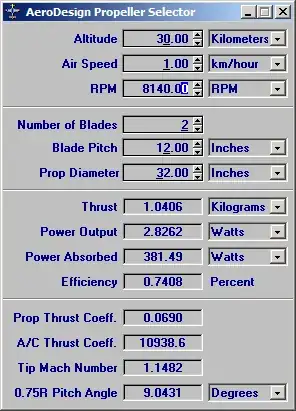
if I take some software to calculate propeller thrust like this Propeller Selector and I calculate this very particular practical example. If I take this propeller which cost 50 euro and this engine which cost 9 euro, then I can fly up to 30 km with only 381 watts of power for 8140 rpm. Fly I mean it will produce 1 kg thrust, which enough to hold 29 grams engine, 349 grams propeller and let say 500 grams for the power source (we can even use a solar panel for it). Calculations are shown in the picture below:

and the same configuration will fly (produce same 1 kg thrust) on the surface with only 47 watts of power and just 1000 rpm.

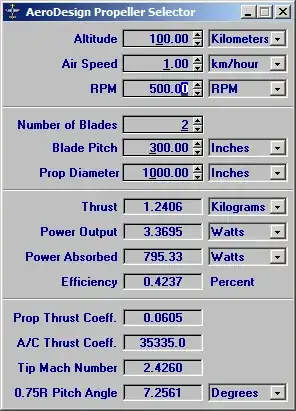
If I go forward, I can calculate that to fly on 100 km I will need 25 meters (1000 inches) diameter propeller and just about 800 watts of power with rotation speed 500 rpm.

I general, we just need big enough propeller, and because of very low air pressure, we will not need a lot of power to make it rotating fast. Also, we can make propeller very thin, because it should not be very strong, because of low pressure as well. Another point, that we can use different propellers for different altitudes, like many stages rockets.

Ultimately, if we make a few kilometer size propeller we can theoretically even fly to Mars and other planets. There are still 30000 atoms per 1 cubic decimeter in space.

UPDATE 1:

Thank you, everyone, for very valuable comments. I will do exact calculations with the real propeller, motor and solar panel to see how high we can go.

The main problems as I understand is the weight of propeller + power source and strength of the material of propeller.

UPDATE 2:

Real calculation of helicopter with solar panels :)

If I take this real propeller which is 6.5 kg and 70 inch diameter, this real motor with 1600W power and these row solar panels with the weight with the weight 4.5 kg for 1350 watt (or 1 kg gives 300 watt) and I add 50% of mass of the solar panel to the mounting of them.

My calculation with the same program (Propeller Selector) shows that it can fly up to 5km taking into account mass of propeller, the mass of motor, the mass of solar panels, the mass of solar panel mounting, max motor power, max propeller rpm, max motor rpm.

If solar panels were 10 times lighter, then 20 km could be reached.

So far, I see only 2 problems:

1. The weight of the solar panel. If we can make it 10 times lighter, then we can reach much higher altitude.

2. This program can give wrong results for altitudes higher than 5-10 km.

Other problems from comments:

• Rotor speed being higher than orbit speed. Calculation shows that it is not necessary and Karman line depends on aircraft weight. So, if we make very lite aircraft/airplane from non-existing/"future invented" material (carbon epoxy, etc.), then Karman line will be higher than 100 km.
• Shock wave when propeller parts are moving faster than sound. One comment was, that it is not a big problem if air density is very small. So we can start with low speed on the ground and reach high speed propeller when we reach higher altitude.
• The strength of the material. In my last picture with 25 m (1000 inch) propeller, if I calculate acceleration and g-force it will be 3500g, yes, 10 times more than normal helicopters (Mi-26 helicopter with 32 m propeller and 132 rpm). But, considering that piston inside V8 Formula 1 car engine works with 8500g, then it is kind of feasible). Maybe they do not do it for real helicopters because of sound speed, but as I told before, it does not matter at high altitudes.

Answer 1

A 25m diameter rotor has a perimeter of around 78 meters. At that size, at 500rpm, the rotor tips would be going in excess of 1,400mph.

At those kind of speeds, even though it doesn't take much power to get a very light rotor going, there is still an awful lot of force involved which has to be handled by the materials to prevent them literally tearing themselves apart.

Answer 2

At 100 km altitude, you get to the Karman line. This is the altitude where you have to fly at orbital speed to get sufficient lift. This definition is based on the lift equation, which applies to all airfoils including that of a helicopter rotor.

So in a helicopter at 100 km altitude, your blades have to travel at orbital speed (27,000 km/h or 17,000 mph) to generate enough lift.

Because the blades rotate, the inside of the blade travels at a lower speed and the outside travels at a higher speed. Taking the average, the midpoint of your blades would have to revolve at 27,000 km/h.

If you want to get into orbit instead of having to keep spending energy on hovering, you have to fly at 27,000 km/h. When you do that, the advancing blade moves at 54,000 km/h relative to the air. The receding blade moves at 0 km/h relative to the air. The heating effects alone would be enough to melt your blades in a short time.*

I wouldn't want to cope with the aerodynamics of blades that go from 0 to 54,000 km/h twice per rotation, nor with the centrifugal forces in the rotor system.

*: in a rocket launch, the fairing is usually jettisoned at an altitude of ~100 km, when the heating effect drops below 1 kW/m². The rocket is far below orbital speed at that point (5000 km/h?). Aerodynamic heating scales with the square of the speed, so a helicopter rotor would be subject to 100 times that.

Alternative approach

Approaching from a different angle: at 100 km, atmospheric pressure is 10^-7 bar. So your rotor blades need to have 10⁷ times the area to get the amount of lift you need to hover. Your propeller has an area of 32"x1" (roughly), at 100 km that goes to 32 million sq in = 222,000 sq ft is 20,000 m² is a propeller longer than a Boeing 747. There's no way to make a structure that large within your weight budget. You could increase lift by increasing speed, but then you're back to supersonic propellers.

First principles

The lift of an aerofoil (any aerofoil, including a helicopter rotor) is governed by this equation:

$$L = \tfrac12\rho v^2 S C_L$$

L is the lift force
ρ is the air density
v is the aircraft's speed relative to the air
S is the aircraft's wing area,
$C_L$ is the lift coefficient.

When you go from ground level to 100 km, ρ reduces from 10⁵ Pa to 0.01 Pa (data from atmospheric models discussed here). That means lift also reduces by a factor of 10⁷. You have to compensate for that by either increasing the speed by a factor 10^3.5 or increasing your wing area by a factor of 10⁷, or a combination of both.

Both inevitably increase weight, which means you need more lift. This is a vicious cycle, and at altitudes far below 100 km you get to a situation where no material in existence is light enough to make your helicopter work.

Answer 3

Space is really like this (XKCD What if)

In theory a plane could reach most of the way to space, but it won't be able to reach orbital speeds.

Bottom line, it just isn't practical. Maybe someday a helicopter could lift a rocket up high, which would help a bit, but it really just isn't practical. Also, a balloon might just be better in any case, it can go higher and lift more payload.

Answer 4

The propellor needs to be strong enough not to pull itself apart via centrifugal force. If you go through the math, you find that the maximum stress on the propellor blade will be halfway along its length, and will have the value $$ \sigma = \frac{1}{4}\rho L \omega^2, $$ where $\omega$ is the blade's angular velocity (usually measured in radians/second) and $\rho$ is the density of the material (usually measured in kilograms per cubic meter.) Re-arranging this, we find that the specific strength of the propeller material must be $$ \frac{\sigma}{\rho} = \frac{L \omega^2}{4}. $$

For a 12.5-meter length blade rotating at 500 rpm, this works out to be $$ \frac{\sigma}{\rho} \approx 34 \text{ kN}\cdot\mathrm{m/kg}, $$ which is still within the realm of known materials. However, as you get higher, you'll need to increase either the size of the blades, their rotation rate, or (probably both); and eventually you'll get to the point where you have to build your helicopter blades out of unobtanium.

Answer 5

OrganicMarble touched on this in a comment but I think it deserves an answer as well, since the question doesn't stop at the Karman line (approx. 100km if you're really defining it as the height where the velocity required to generate lift exceeds the orbital velocity).

In simplest terms: just because there's a few atoms of gas present at some height doesn't mean it's acting like a gas does at sea level.

Part of the reason a wing (and make no mistake, a helicopter's rotor is absolutely a wing for these purposes) works at all is because air fills in around it. Air rushes in behind it because air molecules fly around and bounce off of each other and fill up space, and so you can keep pushing down air, which in turn pushes up your wing and whatever is attached to it.

This is really aerodynamically important! The wing doesn't have to literally hit a molecule of air to get involved with that molecule, because the molecules are involved with each other. The wing or rotor disc can use a lot of the air around it!

As height increases and the ambient pressure drops (because gravity drags the air down, and there's only so much air around for the other air to essentially stand on top of) that space-filling effect really isn't happening anymore. The air molecules are doing a lot less bouncing (their mean free path is longer) and so once you push them out of the way there's nothing left to push down on. You essentially only interact with the air you hit.

All that is to say this premise

Ultimately, if we make a few kilometer size propeller we can theoretically even fly to Mars and other planets. There are still 30000 atoms per 1 cubic decimeter in space.

is wrong. Once you can't fill in air for the propeller to grab, you're essentially just as likely to bounce your 30,000 atoms off the top than the bottom. This doesn't matter for something like a vacuum pump, because if the molecule bounces off the top eventually it should get another chance to come back to the pump by bouncing off the vacuum chamber's walls. When you're in open space, it means the net force your propeller can create is zero.

If you're an experimentalist, this is trivially true just by observing that the Space Shuttle had giant wings and completely ignored the lift that it generated while it was in Low Earth Orbit. The International Space Station also has giant wings (the solar arrays!) and mostly thinks of those in terms of drag. Think of how many cubic decimeters the ISS has intersected in its decades on orbit! (Lift generation for both is actually more favorable for both of these than for your helicopter, since they move sideways at terrific speeds, thus encountering regions where they haven't already hit all the available air molecules.)

Answer 6

We don't fly to space with helicopters because we can't. We would if we could, believe me.

Aside from all the very valid concerns raised by others, the question doesn't properly account for weight*. Maybe your 32 inch diameter propeller weighs 349 grams, but the 10m one certainly doesn't. Oh no! Now 1kg thrust won't lift it at all! So you need more power! So you need more fuel/energy! So you need more thrust...

Solar panels won't solve your problem. They sound great when you don't need a lot of power, but their specific power (Watts per kilogram) doesn't hold up versus something like a jet turbine or rocket engine. Batteries also don't have specific energies (Joules per kilogram) comparable to hydrocarbon fuels yet.

The world's current helicopter altitude record is a bit less than 41,000 feet. Ultimately helicopters just can't put enough power into the air to continue lifting themselves. They all eventually hit a thrust-to-weight ratio of 1, even though a turbine helicopter has vastly more power available than the helicopter you're proposing.

Why does the proposed Mars helicopter work while yours wouldn't? Because it doesn't go very far. The power requirements favor a small helicopter, since the weight drops so much more rapidly than the thrust as it scales down, but the flight times being talked about are about 90 seconds (much like terrestrial drones!) So it couldn't make it from an Earth Sea Level equivalent altitude to the proposed Mars Equivalent altitude; it would run out of energy before it got there.

(*I see in comments on other answers that you've said it's "just a matter of propeller and solar panels weight." It is, but you can't make them arbitrarily light. There's no scaling law that even suggests they'll get dramatically lighter over the next couple decades.)

Answer 7

The propeller would still weigh a lot!

• You don't want it to bend 90 degree in direction of flight or bend in opposite direction of rotation, which requires some stiffness which does not come cheap in terms of weight. it cannot be very thin.

• Also I would assume at the base it must me as thick(or similar) as your 81cm propeller base at sea level to support the weight of your aircraft. Let us assume a linear drop in thickness to the tips. Even without calculation I can tell you it will be very heavy.