I'm having a problem with the insertion from a LEO orbit into a moon orbit/ moon flyby in my gravity simulator. I use the calculations listed below. I think it is due to the fact that the moon pulls the object inwards as it gets to the moon, which has to be compensated for, though sadly I do not know how to tackle this problem. I got the formulas from StackExchange page
So far I have tried to calculate the gravitational potential energy of the insertion orbit, though not having any luck. I have tried manually adding a bit of deltav and got to see that about 5-16 would do the trick, depending on target altitude.
Would anyone have a good way of correcting for the moon's pull in the transfer calculation?
Images:
NOTE: the first two images are relative to the moon.
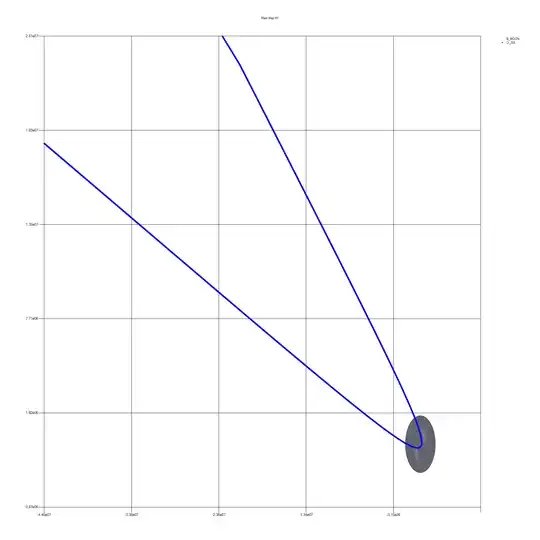
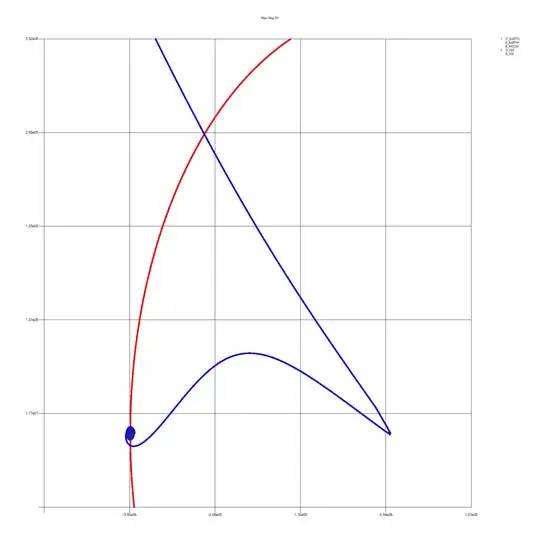
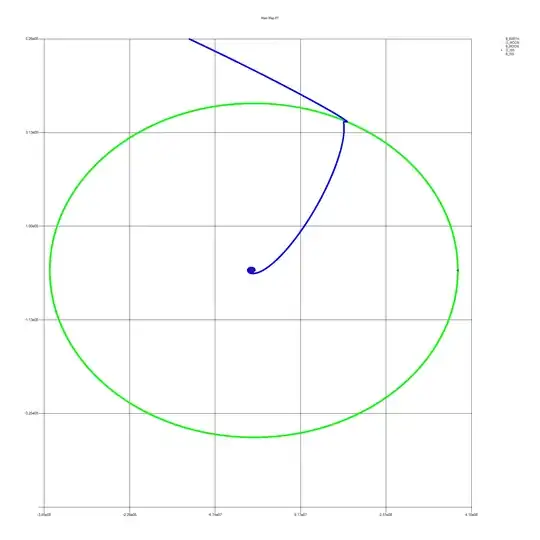
Calculations:
insertionheight = injected radius from moon (+moon.radius)
R1 = radius to LEO (from earth)
R2 = radius to Moon Orbit (from earth) + insertionheight
vLEO = Math.Sqrt((G * earh.mass) / R1)
vP = Math.Sqrt((2 * (R2-insertionheight) * G * relativeobj.mass) / (R1 * (R1 + R2-insertionheight)))
vInject = vP - vLEO
vLLO = Math.Sqrt((G * targetobj.mass) / (insertionheight))
vM = Math.Sqrt((G * relativeobj.mass) / (R2 - insertionheight))
vA = Math.Sqrt((2 * R1 * G * relativeobj.mass) / (R2 * (R1 + R2)))
vL = Math.Sqrt(Math.Pow(vM - vA, 2) + (2 * G * targetobj.mass) / (insertionheight))
vInsert = vL - vLLO
TOF = pi * Math.Sqrt(Math.Pow((R1 + (R2-insertionheight))/2.0, 3) / (relativeobj.mass*G))
The same but as typed in C#:
double R1 = (movedobj.location.placevector - relativeobj.location.placevector).Length;//Math.Sqrt(Math.Pow(movedobj.location.placevector.X - relativeobj.location.placevector.X, 2) + Math.Pow(movedobj.location.placevector.Y - relativeobj.location.placevector.Y, 2) + Math.Pow(movedobj.location.placevector.Z - relativeobj.location.placevector.Z, 2));
double insertionheight = 200000 + 1737000;
double R2 = (targetobj.location.placevector-relativeobj.location.placevector).Length + insertionheight;//Math.Sqrt(Math.Pow(targetobj.location.placevector.X - relativeobj.location.placevector.X, 2) + Math.Pow(targetobj.location.placevector.Y - relativeobj.location.placevector.Y, 2) + Math.Pow(targetobj.location.placevector.Z - relativeobj.location.placevector.Z, 2)) ;
double vLEO = Math.Sqrt((G * relativeobj.mass) / R1);
double vP = Math.Sqrt((2 * (R2) * G * relativeobj.mass) / (R1 * (R1 + R2)));
double vInject = vP - vLEO;
double vM = Math.Sqrt((G * relativeobj.mass) / (R2));
double vA = Math.Sqrt((2 * R1 * G * relativeobj.mass) / ((R2) * (R1 + R2)));
double vLLO = Math.Sqrt((G * targetobj.mass) / (insertionheight));
double vL = Math.Sqrt(Math.Pow(vM - vA, 2) + (2 * G * targetobj.mass) / (insertionheight));
double vInsert = vL - vLLO;
double TOF = pi * Math.Sqrt(Math.Pow((R1 + (R2- insertionheight))/2.0, 3) / (relativeobj.mass*G));
double ttransfer = (2 * pi - (pi - Math.Sqrt(G * relativeobj.mass / Math.Pow(R2, 3)) * TOF)) / (2*pi / ((2 * pi * R1) / (Math.Sqrt(G * relativeobj.mass / R1))) - 2 * pi / (2 * pi * R2 / (Math.Sqrt(G * relativeobj.mass / R2))));
Thanks all in advance.