I'm the author of the TPUG article.
The "BILL GATES SUCKS" message isn't really an Easter egg; that was just a conceit of mine to make the article a bit more interesting and to turn it into a bit of a puzzle. Here's how it works and how it was created:
In any given infinite sequence random numbers, it's a mathematical certainty that a given subsequence of numbers will appear at some point. For example, if you repeatedly roll a normal six-sided die, then at some point you are bound to roll the sequence 6, 5, 4, 3, 2, 1—though it might take you hours of rolling before this happens. Similarly, if you had a hypothetical 26-sided die labelled with the letters of the alphabet, then repeatedly rolling it you would expect at some point to form the words "BILL", "GATES", and "SUCKS". Again, this might take you hours, days, or even months of continuous rolling.
The "random" number generator in the Commodore 64 and its brethren isn't truly random, but it's close enough that you can still expect to find arbitrary subsequences in its output. The only problem (or in my case, feature) with it is that, every time you turn on the machine, it always produces the same "random" sequence of floating-point numbers, all between 0 and 1. The random sequence can be changed only by seeding the generator with a numeric value. Each seed value causes the generator to produce a different random sequence.
With this in mind, I set out to find three seed values such that the first five or six numbers of their respective sequences, multiplied by 22 and rounded down to the nearest integer, correspond to the the alphabetic indices of the letters in the words BILL, GATES, and SUCKS, followed by a zero. For example, there is some seed value that makes the C64 random number generator start off with a sequence of floating-point numbers x1, x2, x3, x4, x5 such that ⌊22x1⌋ = 2, ⌊22x2⌋ = 9, ⌊22x3⌋ = 12, ⌊22x4⌋ = 12, and ⌊22x5⌋ = 0; note that B is the 2nd letter of the alphabet, I is the 9th, and L is the 12th. (I multiply by 22 because that's one more than the index of U, the alphabetically last letter in the message.)
These three seed values were found by writing a BASIC program that iterated through all possible integer seed values until it found one that generated the correct sequence:
0 k=1:f=22
10 inputw$
15 w$=w$+chr$(64)
20 l=len(w$):dimw(l)
30 fori=1tol
35 printi
40 w(i)=asc(mid$(w$,i,1))-64
50 next
60 i=-1
70 a=rnd(i):j=k
90 printi:ifj>lthenend
100 ifint(rnd(1)*f)=w(j)thenj=j+k:goto90
110 i=i-k:goto70
120 ifi>-1theninputi:ifi>-1theni=-i
130 i=rnd(i)
140 i=int(rnd(k)*f)
150 ifi=0thenprint:end
160 printchr$(i+64);:goto140
To use it, first think of a short word you want to "encode", and change the value of f in line 0 to the index of the alphabetically last letter in the word plus one. Then run the
program and type in the word. The program will then test each seed value, printing them out as it goes. It stops when it finds a seed that prints the string.
The program looks a bit odd, but that's because it's optimized for speed. (For instance, I prefer using variables and gotos to constants and for loops.) I compiled it using the Blitz! compiler and ran it using the VICE emulator in warp mode. This way seeds can be found within a few minutes or hours. Runtime on a real C64 would have been tens or hundreds of times longer.
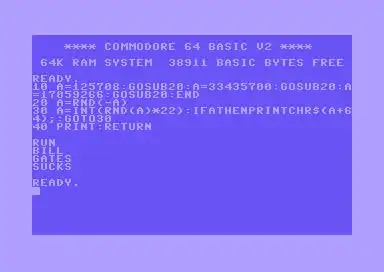
Once I had the three seed values, it was a simple matter to write a short BASIC program that used them to seed the random number generator three times and print out the generated letters.
Ain the code. – JimmyB Aug 04 '17 at 14:24