Is integer arithmetic really slower than float with (early) MS-BASIC?

Question

This question is based on a comment by Neil on another question regarding integer-multiplication:

Do you have any citations for your claim that most MS-BASIC integer multiplication was done by turning into floats? Seeing as how the majority of processors before 80486DX (8,16 or 32 bit) didn't have any floating point processors, this would have been extremely slow.

I think they didn't bother doing fast integer multiply for simplicity's sake, and also because anyway the BASIC is slow, but convenient. If you wanted speed in a game, you used asm for the main game loop, with a possible BASIC initialization where complex & slow operations weren't a problem. — Jean-François Fabre, Mar 18 '20 at 23:09

Raffzahn · Answer 1 · 2022-06-07T18:53:27.167

Do you have any citations for your claim that most MS-BASIC integer multiplication was done by turning into floats?

Beside having lived thru it, or noting that the source of MS-BASIC doesn't contain any integer routines (except for conversion)? (*1)

I assume the most simple and obvious proof would be to just try it. Commodore 8 bit machines are a great tool here as their BASIC provides access to a simple real time clock. The variable TI(ME) is incremented every 1/60th second. Since the effect is rather large, already a few seconds of measurement should deliver a valid result.

So lets setup a test program:

    100 REM >>> VARIABLE SETUP <<<
    110 A=3:B=7:C=0
    120 A%=3:B%=7:C%=0
    130 I=0
    140 T1=0:T2=0:T3=0:T4=0:T5=0
    150 TI$="000000"
200 REM &gt;&gt;&gt; MEASUREMENT    &lt;&lt;&lt;
210 T1=TI
220 FOR I=1 TO 1000:NEXT I
230 T2=TI
240 FOR I=1 TO 1000:C=A*B:NEXT I
250 T3=TI
260 FOR I=1 TO 1000:C%=A%*B%:NEXT I
270 T4=TI
280 FOR I=1 TO 1000:C%=3*7:NEXT I
290 T5=TI

300 REM &gt;&gt;&gt; PRINT RESULTS  &lt;&lt;&lt;
310 TL=T2-T1
320 PRINT &quot;LOOP :&quot;;TL
330 PRINT &quot;FLOAT:&quot;;T3-T2-TL
340 PRINT &quot;INT  :&quot;;T4-T3-TL
350 PRINT &quot;CONST:&quot;;T5-T4-TL

Workings:

The program defines 3 variables A, B and C as float and integer. A and B are preloaded with values (3; 7), while C is set to zero. This is done to have all variables ahead of used, so no allocation has to be done during use.
TI is as well zeroed to avoid any overflow error (*2).
A first time stamp is saved in T1.
An empty loop is performed to measure the FOR/NEXT overhead.
A time stamp is taken in T2
The measurement for float calculation is done in form of multiplying 3 and 7 from variables a 1,000 (*3) times in a FOR...NEXT loop.
A time stamp is saved in T3,
followed by doing the same with integer variables and
saving the time stamp in T4,
followed doing the same with constant values and
a final time stamp in T5.

Results are printed as difference between the time stamps (T1, T2, T3, T4, T5) for each test, reduced by the time taken for the empty loop.

While I suggest to try it on your own PET, CBM, C64 or C128, it will as well work on emulators. A great tool here could be the PET emulator at Masswerk. It's not only a fine implementation, but also offering a lot of ways for im-/export - including starting a program from a data URL, like with our test program:

Open this fine link to run above test program (maybe in another window)

Doing so should present a result similar to this:

    LOOP : 91
    FLOAT: 199
    INT  : 278
    CONST: 275

The numbers show that using integer variables takes about 40% longer than doing so in float. This is simply due the fact that each and every integer value stored in any of the variables is converted to float before multiplication and the result converted back to integer. Interesting here is that the use of constants does not result any relevant speed up. Here again each constant has to be converted before used. In fact, converting from ASCII to float is even slower than converting from integer - but offset by skipping the need to search for each variable.

Speaking of variable lookup, it's well known, that that the sequence variables are defined in MS-BASIC, does have a huge influence on access time (*4). Swapping the definitions of float (line 110) and integer (line 120) variables does show this effect quite nice:

    LOOP : 91
    FLOAT: 218
    INT  : 259
    CONST: 269

Now the integer malus has shrunk by the effect of variable access and allows us to calculate a close net cost of 30% overhead (259 vs 199 ticks) for type conversion when using integer instead of float.

Seeing as how the majority of processors before 80486DX (8,16 or 32 bit) didn't have any floating point processors, this would have been extremely slow.

Jau, it is. But there are good reasons to do so:

Code size

Additional routines for integer multiply and divide would cost at least a few hundred bytes in code. This may not sound much, but keep in mind, that ROM storage was quite small and developers had to fight for every instruction. But beside the code for multiplication/division, it's even more about

The way BASIC works

MS-BASIC is an interpretative language without any processing ahead of time. Inputted source code gets not prepared in any way beside turned into a more compact storage representation by using single byte symbols for keywords and operators. The method was called 'crunching' by Allen/Gates (*5), other called it tokenization. This process does not analyze any semantics. It's a literal representation of the source.

When the interpreter parses an expression it has no knowledge what type the elements are. Only if all are integer the calculation could be done using integer arithmetic. Thus it is mandatory to do all calculations in float, to avoid any intermediate rounding error (*6).

Of course, the cruncher could have been improved to leave hints to the interpreter, or even transform the expression into a format allowing to use integer operations wherever possible - but this would not only have meant to add a lot of code to already packed ROMs but as well increase RAM usage for BASIC code (*7). Something not really a good idea. After all, these interpreters were designed for machines with a basic RAM size as low as 4 KiB (PET, Apple II, TRS-80 M1, etc.).

So this again comes down to limited memory size of these computers.

And now for something complete different:

Chromatix did go the extra mile to port, modify and try above little test program for the BBC (or better Jsbeeb):

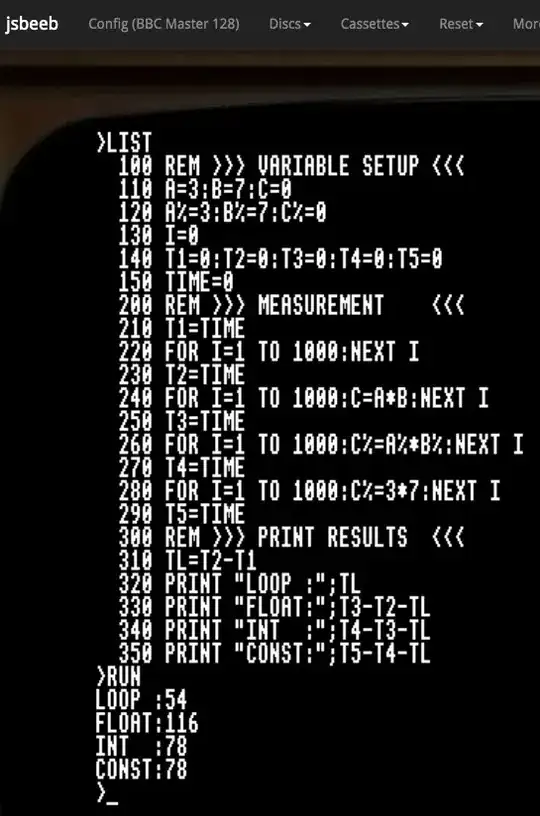
While not really asked for by the Question, I do think it's a worthwhile addition, showing how much a BASIC with proper integer support may gain from using them percent signs.

*1 - To be honest, it's simply much more fun to write some benchmark than simply looking up any old writing.

*2 - TI runs modulo 5,184,000 (24 * 60 * 60 * 60 ) i.e. is reset every 24 hours. Resetting it at the begin of the program will ensure no unintended reset will happen during measurement, thus simplifying calculation to subtraction. Except, TI can not be written, clearing is only possible via TI$. And yes, this destroys any time of day set before, but serious, noone cares for it's value on a PET outside of an application.

*3 - The number 1000 has been chosen to set run time close to 4-5 seconds per measurement. This will give a result large enough to gain valid data but still keep total run time below 30 seconds.

*4 - MS-BASIC stores variables (their structures) in sequence of definition. Lookup is done by sequential search. Thus access time is linear with position/sequence of definition.

*5 - The crunching code was written by Paul Allen.

*6 - Sure, it could start out with with integer and switch for using float as soon as any operation yields a fraction, or a float variable gets involved. Except, this might include backtracking the evaluation stack in case intermediate results (like from grouping by parentheses) exist, which would add even more code.

*7 - It's again important to keep in mind that the crunched BASIC code not only was a direct image of the source, but it must be possible to transform it back into it's source (or at least quite close) form. Reordering an expression is thus not an option - unless stored twice.

I confirm that Oric microsoft basic does that too (storing everything to float). The integers are special types with special variable names (on Oric: I%). They were rarely used in games. I don't remember if we could multiply those. And you're right, I didn't find any generic integer multiplication in the oric rom — Jean-François Fabre, Mar 16 '20 at 22:32
actually every operation was using floats. Addition/subtraction too. excellent answer btw. I'm not sure that ROM size limitations was the real issue, though as noted in my answer, a generic multiplication routine doesn't take a lot of room (https://retrocomputing.stackexchange.com/a/14118/3316). But it's simpler to assume floats for everything, That part is very true. — Jean-François Fabre, Mar 16 '20 at 22:34
@Jean-FrançoisFabre yes, as decribed, the interpreter has to use always float as it can not look ahead in an expression. (for your forst comment, integers are stores as such, not as float. Then again, a variable entry is still 7 byte, no matter if float or integer). — Raffzahn, Mar 16 '20 at 22:41
yes, A=4/2 and A=3/2 will always produce a float no matter what. even if the result is integral in the end. I banged my head on the wall when I wrote an Oric basic to C converter because in C 3/2 yields 1... Good luck finding the bugs in the converted games... — Jean-François Fabre, Mar 16 '20 at 22:44
The Integer variables in MS BASIC, at least on the 6502 variant, have only two real application: 1.) in some (fairly rare) situations assigning a result to an integer variable might save you one call to INT(X) when you need to throw away a fractional part, and 2.) and much more importantly, while simple integer variables take as much RAM as floats, integer arrays can be a big space saver - they take only 2+2n bytes for n elements, not 2+5n as float arrays do. Of course this has to be balanced against the slower processing and the additonal "percent" characters in your code. — TeaRex, Mar 17 '20 at 12:35
@TeaRex Yes, true. This is where MS-BASIC variants with DEFINT capability can realize the benefits without the code cost of adding a type qualifier. — Raffzahn, Mar 17 '20 at 12:43
"Interesting here is that the use of constants does not result any relevant speed up" - luck basically, you're using a one-byte ASCII const, as opposed to a one-byte var name. The rest of the conversion is the same. I'm curious what happens if you change 3 to 3000 etc. — Maury Markowitz, Mar 17 '20 at 15:02
For giggles, I wrote a 3-line program that set up 10 vars = 10 and then FOR I=1 TO 10000. On a C64 emu, that's 18.4 seconds. Adding a line 5 with I=0 reduces it to 14.4 seconds! Clearly the Atari approach is better and goes to show just how bad the FP code is. — Maury Markowitz, Mar 17 '20 at 15:06
@MauryMarkowitz Jup. That (400µs) is the time it takes to iterate over each variable in the list. With complex programs it was important to analyze the variables used and their access frequency to define them in the right order. This could bring a dramatic speed up. — Raffzahn, Mar 17 '20 at 15:16
@MauryMarkowitz regarding longer constants: Not much. fetching an additional character from code isn't a big deal. Most of the additional time comes from conversion. Just try it in the emulator. A great tool BTW. — Raffzahn, Mar 17 '20 at 15:18
An optimized integer-multiply routine might be a bit bulky, but one could be written quite compactly and still blow the socks off the cost of int->float->int. I wonder how much ROM it would have actually cost to treat a floating-point value whose exponent was zero as a 16-bit or 24-bit integer (depending upon whether PEEK/POKE can accept negative values)? — supercat, Mar 17 '20 at 20:41
@supercat As explained the main problem aren't the integer math routines itself, it's about the way (MS) BASIC works. When evaluating an expression like A%=B%/C%*D The result of A%/B% has to result in an intermediate float result to avoid rounding errors. Also, it's not about how a BASIC could operate, but how MS-BASIC does. Other BASICs did show many great ways to improve here - all at cost of more complex interpreters ofc. — Raffzahn, Mar 17 '20 at 21:39
@Raffzahn: Division needs to be done with floating-point, but for addition and multiplication, it should be practical to say "if both arguments are integers, try an integer add, subtract, or multiply; if that overflows, or if either operand wasn't an integer, convert to float and process that way". Even if that was only done for constant conversion, addition, and subtraction (not multiplication) that would make a huge difference to performance. — supercat, Mar 17 '20 at 21:45
@Raffzahn: Alternatively, and perhaps more simply, performance could also have been improved if floating-point values didn't use an "implied leading one" format, and addition, subtraction, or comparison would shift the smaller value left as needed to match the exponent of the larger, and left the result with that exponent. If all integers start out with an exponent such that one ULP has the value 1, that would avoid the cost of to normalizing and aligning numbers, which together form a major part of the cost of floating-point math. — supercat, Mar 17 '20 at 21:53
@supercat Again, this is not about what could have been done, but an explanation what was done. — Raffzahn, Mar 17 '20 at 22:26
To validate your test program, I modified it very slightly to run on a BBC Master: https://www.dropbox.com/s/yn0zzavdyiv8uxq/Screenshot%202020-06-28%2000.10.44.png?dl=0 This demonstrates that on a BASIC which does have native support for integers, they do have a performance benefit over floats. — Chromatix, Jun 27 '20 at 21:14
Neat answer, as usual. Richard Russell's implementations of BBC BASIC have used variants for unsubscripted variables since 1981. It means that integers stay as integers for as long (and as fast) as possible, at the cost of using the same amount of memory as a float. — scruss, Dec 25 '20 at 22:11
The support for integer-type variables other than arrays is somewhat curious. While the easiest way to support integer-type arrays might have been to support integer-type variables, all non-array variables use the same amount of space regardless of type; using integer types for non-array variables will not only make things slower, but it won't save any variable space. The the effort spent on integer types, could, IMHO, have been better spent on DPEEK/DPOKE and code to optimize math with operations involving small integers. — supercat, Dec 26 '20 at 19:15
For Commodore BASIC programs, it's helpful if you list them out them in lower case, rather than than upper case, since in lower case they can be copied and pasted directly into VICE. — cjs, Jun 08 '22 at 01:18
The HP BASIC that I first learned to program with in 1973 didn't even have integers - everything was a float. I wonder if the earliest versions of MS BASIC worked the same? — Mark Ransom, Jun 17 '22 at 23:27
@MarkRansom AFAIK the original 4k and 8k Altair BASIC did not offer integer variables. 4k BASIC had only numeric variables (skalar and array) while 8k also added strings. The later 12k Extended BASIC added Integer and 64 bit Double. MS-BASIC is following DEC's BASIC PLUS in design. HP BASIC is as well an early one and, like BASIC PLUS modelled after Dartmouth BASIC, which also offered only float. — Raffzahn, Jun 18 '22 at 00:35

score 9 · Answer 2 · answered Mar 18 '20 at 00:29

As noted, MS-BASIC implementations such as those found in the Commodore used floating-point math for everything, and the performance implications of this were severe.

Consider the following program:

10 TI$="000000"
20 A=32768:B=1:C=2
30 FOR I=1 TO 1000:A=A+B-C:NEXT
40 PRINT TI,A

Testing on VICE emulating an NTSC C64, the above code takes 320 ticks (5.33 seconds). Changing the constants in the first line to A=32768:B=16385:C=16384 reduces this time to 280 ticks (4.67 seconds). That's a 12% speed difference for the overall loop, merely as a consequence of the values of the numbers involved. Considering the difference in magnitude between the FOR loop's index and step size, the 12% speed difference represents a pretty huge difference in performance, purely as a result of the amount of time spent shifting floating-point numbers.

Is integer arithmetic really slower than float with (early) MS-BASIC?

2 Answers2

Linked