Distribution of the Normal Force

Question

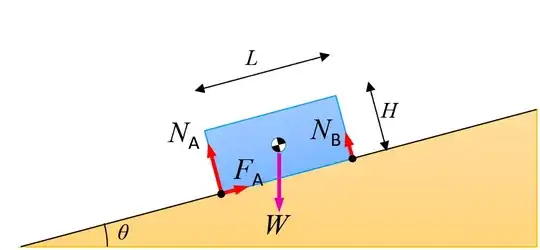
Is there an equation that gives you how the normal force is distributed? In particular, I am considering a basic example with a rectangular object at rest on an inclined plane. I think the biggest part of the normal force is applied at a distance down the incline from the center of mass of the object equal to the coefficient of friction times the distance between the object's center of mass and the surface. I think this case is basically 2D. How do you find a model of the different amounts of force between the object and the surface? Or if that is just really super complicated, how do you find the maximum amount of force at that point/line from 3 sentences ago, or at least what kind of math is used?

Also, please let me know if I am phrasing things poorly or if there would be a good source to learn about this.

Answer 1

You can say some things about the force, mainly that the torques from all the forces must sum to zero since the object is at rest.

But otherwise, no. The specific forces depend on the specifics of the surfaces. Imagine having two surfaces engineered to be very flat. But there is a tiny, tiny rock between the surfaces. A huge force will be concentrated on that point (with some other forces near the edge).

You could assume that the surfaces are nearly flat and the pressure across the entire area is nearly constant. But for real surfaces, it may not be.

In other words, there are many possible force distributions that are all consistent with the object remaining at rest.

Answer 2

What you are thinking of definitely could be made into a coherent set of things to do/solve. However, it quickly spirals out of control once you look at how the actual real world physics deviates from the idealisations we are making.

In particular, you are assuming that this rectangular object is perfectly flat, as is the inclined plane. Neither could be true. In reality, you can take microscopic pictures of those surfaces and see that they are jagged. The forces are concentrated on the spots where the jagged parts mesh with each other.

Then consider an idealisation whereby the perfectly flat rectangular object is propped up on the inclined plane at only two points. Then by considering principle of moments, you can figure out the forces. Simply move where the contact points are, and you can get a distribution of forces.

It will be a lot of work, when in fact it does not matter what the distribution is, as long as all the relevant properties are obeyed.

Answer 3

Your intuition is correct. In general, for a flat-to-flat contact, you can assume the contact normal is concentrated at the edges. There will be two contact normals because the part is can't rotate as well as interpenetrate.

And now you apply the balance of forces and torques to find the values of the contact normal $N_A$ and $N_B$ as well as the friction $F_A$ required to keep the block stationary

Looking from a rotated coordinate frame along the ramp you have

$$ \begin{aligned} N_A + N_B - W \cos \theta &= 0 \\ F_A - W \sin \theta &= 0 \\ \tfrac{L}{2} N_B - \tfrac{L}{2} N_A + \tfrac{H}{2} F_A & = 0 \end{aligned} $$

which is 3 equations and 3 unknowns (the two normal forces and friction). The solution is

$$ \begin{aligned} F_A &= W \sin \theta \\ N_A &= W \left( \tfrac{1}{2} \cos \theta + \tfrac{H}{2L} \sin \theta \right) \\ N_B &= W \left( \tfrac{1}{2} \cos \theta - \tfrac{H}{2L} \sin \theta \right) \\ \end{aligned} $$

Please note that the difference between $N_A$ and $N_B$ is due solely to the height of the center of mass above the ramp $\tfrac{H}{2}$.

You can even calculate the tipping condition, which happens when $N_B=0$ which leads to the requirement that $H \leq L \cot \theta$.