0

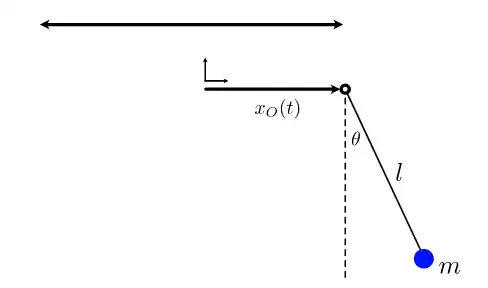
I was trying to find the Eqn. of Motion for the following system (a jiggle pendulum):

Using the Lagrangian and the Euler-Lagrange-Eqn., I ended up with: $$\ddot{\theta} + \frac{g}{l}\sin{\theta} = -\frac{1}{l}\ddot{x_O}\cos{\theta}$$

While it is much easier to solve this eqn. numerically, I was wondering how one would go about solving this analytically. I was trying to solve this eqn. with the following definitions and initial conditions : $$x_O(t) = \sin{(4\pi t)}$$ $$l = 0.2[m]$$ $$\theta(0) = 0$$ $$\dot{\theta}(0) = 0$$

So the eqn. that I have to solve would look like this: $$\ddot{\theta} + 5g\sin{\theta} = 80\pi^2\sin{(4\pi t)}\cos{\theta}\tag{1}$$

But because of my highly limited knowledge, I have hit a roadblock since I have no idea how one would solve a second order nonhomogenous differential eqn. involving trig functions.

During my search on the Internet, I found things like elliptical integrals, complementary functions and particular integrals but I did not quite understand how I should use them.

TL;DR: I would like to solve the second order nonhomogenous diff eqn. marked $(1)$ with the conditions mentioned above it.

Qmechanic
  • 201,751
Donato Paul Thayalan
  • 1
  • 1
    Does this answer your question? Solution to pendulum differential equation – Roger V. Jun 07 '22 at 14:59
  • 1
    I don't know if this one in particular can be solved analytically, but keep in mind that most non-linear differential equations can't be solved by hand. Sometimes a "partial" solution can be found, by lowering the order of the equation, or a full solution can be found but within the limits of an approximation (here it'd be the small oscillations approximation). – Miyase Jun 07 '22 at 15:03
  • @RogerVadim I could try using approximations but I asked this question in view of how would one purely analytically solve the diff eqn. as it is. But thanks alot! :) – Donato Paul Thayalan Jun 07 '22 at 15:11
  • If you read through the answers to the linked question, they specify that only some non-linear differential equations are exactly solvable (and it very much depends on what one qualifies as an exact solution - do special functions count? Does a numerically tabulated solution count?) – Roger V. Jun 07 '22 at 15:15
  • The "duplicate" proposed by @RogerVadim doesn't involve the driving term, and so it seems to me that this question is fundamentally different. – Michael Seifert Jun 07 '22 at 20:02
  • @RogerVadim: Sorry, didn't mean to offend. But I simply don't think this question is close enough to that older one to be closed as a duplicate, and I wanted to offer a different perspective for those who might happen across it in the "close votes" queue. I was under the impression that this was acceptable behavior (see the third bullet point in the accepted answer there.) – Michael Seifert Jun 07 '22 at 20:36
  • @MichaelSeifert fundamentally is certainly an exaggeration, and fingerpointing at me for suggesting that it might be a duplicate seems unnecessary as well. Apart from that, the point seems rather mundane. – Roger V. Jun 07 '22 at 21:03

0 Answers0