2

I am looking for a map or plot of the gravitational strength in the solar system. In an ideal world there should be something like google earth to move around in the solar system, zoom in and out and get an visual overview over the field strength in different points in the solar system.

I didn't even find good pictures/plots via google which show different regions of the solar system. So I would appreciate any material about this.

Edit

Here is a map of the solar system which comes close to what I want in the ideal case, but It doesn't have any information about the field strength distribution...

http://www.solarsystemscope.com/

Abhimanyu Pallavi Sudhir
  • 6,140
Julia
  • 1,692
  • In general gravity gets stronger near mass... – DilithiumMatrix Jun 28 '13 at 19:03
  • That's clear. I just want a kind of snapshot where I can go to any point in the solar system and see how strong the field strength is compare it to other points and have it visualized in some reasonable way... – Julia Jun 28 '13 at 19:20
  • 2
    I would be surprised if such a thing existed. Why not calculate gravity at the locations you are interested in, and compare? – DilithiumMatrix Jun 28 '13 at 19:39
  • "I just want a kind of snapshot" But the planets are in constant motion... Do you want a solar system simulator (virtual orrery) overlaid with the combination of all the gravitational fields? – Mitchell Porter Jun 29 '13 at 08:09
  • Perhaps if you wrote to someone like John Walker, programmer of http://fourmilab.ch/solar/ ... he might be able to add it as a feature. – Mitchell Porter Jun 29 '13 at 08:14
  • @MitchellPorter Sure, that would be even better. But a snapshot of a given time would be sufficient. I want to have for a high school physics course such that students can browser through the solar system and see the real values and directions of gravitational field strength visualized in some way and even the numerical values when moving the mouse over a given point... – Julia Jun 29 '13 at 08:17
  • 4
    Like this: http://xkcd.com/681_large/? – Abhimanyu Pallavi Sudhir Jun 29 '13 at 08:28
  • Or like this: https://www.khanacademy.org/cs/gravity/1011456374? – Abhimanyu Pallavi Sudhir Jun 29 '13 at 08:36
  • Or like this: https://www.khanacademy.org/cs/spin-off-of-gravity-without-acceleration/1742605497? – Abhimanyu Pallavi Sudhir Jun 29 '13 at 08:36
  • OP - what exactly do you mean by the gravitational strength? Are you referring to the local acceleration or are you considering the strength of the gravitational bonding? If the latter, only considering the sun and the planets, or is the whole Milky Way and the Andromeda galaxy etc included? Gravitationally you are much stronger bound to Andromeda than you are to earth... – Johannes Jun 29 '13 at 12:02
  • I want the gravitational force on a small test body or independent of its mass the gravitational acceleration $G \frac{\cdot M}{r^2}$. In this case only the influence of the sun and planets should be relevant. I don't see why one has to consider Andromeda for this (though its large mass, due to its large distance the effect seems to be neglectible). – Julia Jun 29 '13 at 16:07

2 Answers2

3

I'm going to work with gravitational potential, a scalar, rather than the gravitational field, a vector.

The deepest gravitational potential well in the solar system is that of the Sun. The next deepest well is that of Jupiter, but it is only 1% as deep. Earth's is 3000 times shallower.

Suppose all the planets happened to line up in a row, but with their correct spacing based on the semimajor axis of their orbit. Then the gravitational potential along that line would look like this:

enter image description here

The horizontal axis is in astronomical units. The vertical axis is gravitational potential, normalized so that the potential at the center of the Sun is -1. That is 50 times further down than the graph goes.

The little dip of a few pixels at 1 AU is Earth's well, superposed on the Sun's well. You can also see an even smaller dip to the left around 0.7 AU which is Venus. Mercury and Mars's wells are too small to see. The four large dips are Jupiter, Saturn, Uranus, and Neptune.

The planets have such small radii compared with their distances from the Sun that their gravitational wells are basically just spikes when you look at the whole solar system out to 32 AU.

We can zoom in to the vicinity of Earth to look at its well in more detail:

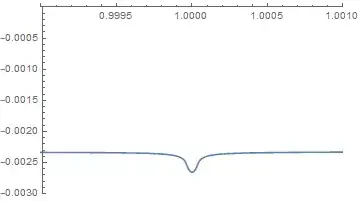
enter image description here

At this scale, the Sun's well appears flat.

Here is a greyscale density plot of the gravitational potential in the ecliptic plane showing the outer planets Jupiter, Saturn, Uranus, and Neptune, in their relative positions today:

enter image description here

The Sun is at the center but its well has not been included because it makes it impossible to see the planets' wells. (They are too shallow by comparison, and there aren't enough shades of gray.) The planets' wells look big and blurry here because I've taken the logarithm of the potential to make the wells less spiky. Otherwise, you'd just see a pixel or two for them. The other planets' wells don't show up because their wells are so shallow.

G. Smith
  • 51,534
1

To describe our solar system, Newton's theory of gravity works very well. Thus, as highlighted by G. Smith, the "gravitational strength" can be evaluated in terms of Newtonian potential $\phi(d)=-\frac{GM}{c^2d}$, that is, gravitational energy per unit of mass caused by the presence of mass $M$ at distance $d$.

Please note that I have explicitly included the term $c^2$ (c=speed of light) so that we have a potential ranging from -1 to 0 (i.e., energy and mass have same units according to the famous $E=mc^2$). This is because gravitational energy may be viewed as intrinsically negative, with maximum value of 0 for an observer at very large distance from $M$ ($d \rightarrow \infty$ "infinity").

According to NASA Sun fact Sheet NASA Planetary Fact Sheet data, I have produced a graph showing the module of the gravitational potential caused by the Sun and each planet in our solar system as well as the total potential (sum of all values, since the potential is additive).

As you can see, the Sun accounts for almost all gravitational potential: this is the reason why I used a logarithmic scale for $\phi$ (thus the choice to display its absolute value, since it is intrinsically negative). Such scale allows one to spot almost imperceptible spikes due to Venus, Earth, Mars, and a few notable spikes due to Jupiter, Saturn, Uranus and Neptune.

Finally, note that the maximum value for $|\phi|$ in the solar system is about $3\cdot 10^{-6}$ (at the center of Sun, $d=0$). This value is very small $|\phi|\ll 1$ (weak gravity), and this is the reason why Newton's law works well (see the "Limitations" section).

The full python code I used to build the graph is here. Enjoy!;-)

![Newtonian gravitational potential in the solar system

QuantumBit
  • 11