Is the decoupling matter/radiation in the universe evolution due to the electron/nuclei recombination or to the *density* decrease or to *both*

Question

Is the matter/radiation decoupling in the evolution of universe due to

-the electron/nuclei recombination (because temperature decreases), so that photon-matter cross-section reduces since there is less energy

or

-the density decrease, so that photon-matter cross-section reduces

or

-due to both ?

(I have read Nature of decoupling of matter and radiation , but it is less explicite that my question)

Answer 1

The current hydrogen density in the universe is approximately $0.04 \times 6$ atoms per cubic metre. If we wind the clock back, this number goes up as $(1+z)^3$, where $z$ is the redshift.

The CMB formed at $z \sim 1100$, thus the number density of electrons in the universe just prior to this was $n_e \sim (1+1100)^3 \times 0.04 \times 6 = 3.2\times 10^{8}$ m$^{-3}$.

The Thomson scattering cross-section is $\sigma = 6.6\times 10^{-29}$ m$^2$ and the mean free path of a photon is $l =(n\sigma)^{-1} = 4000$ light years.

At that time, the universe was 400,000 years old. Thus the mean free path was 100 times smaller than the characteristic "size", $ct$, of the universe.

So let's just imagine that temperature wasn't a factor. As the universe expands, the mean free path increases as $l \propto a^3$, but since the universe is matter dominated, $a^3 \propto t^2$ and so $l \propto t^2$. But since the "size" of the universe increases as $ct$, then the ratio of mean free path to size also increases as $t$. Thus when the universe is about 100 times older it will become transparent to radiation.

In other words, if the hydrogen had remained ionised, then the expanding universe would not have become transparent to radiation until the scale factor had increased by another factor of $10^{4/3}$ and was approximately 40 million years old (at a redshift of about 50).

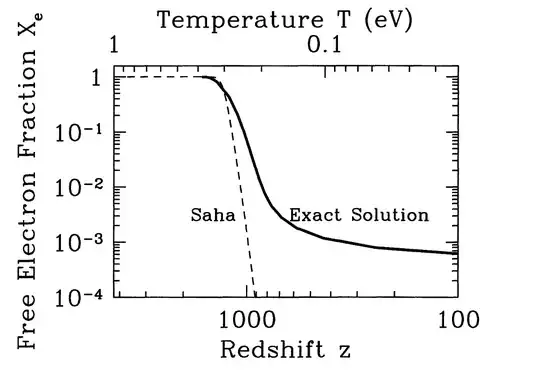
In contrast, the actual transition from opaque to transparent takes place over a relatively short space of time (or small range of redshifts) of a few tens of thousands of years, since the ionisation fraction of the hydrogen is highly sensitive to the decreasing temperature. Thus the hydrogen is essentially all ionised at redshifts above around 1500 and then drops below an ionisation fraction of $10^{-3}$ at $z \sim 300$ (see plot below), long before the density became low enough to render the universe transparent (see below).

So the answer is temperature.