2

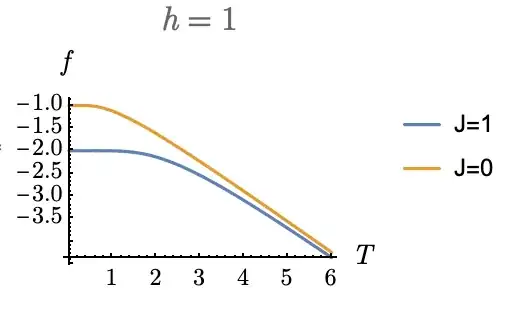
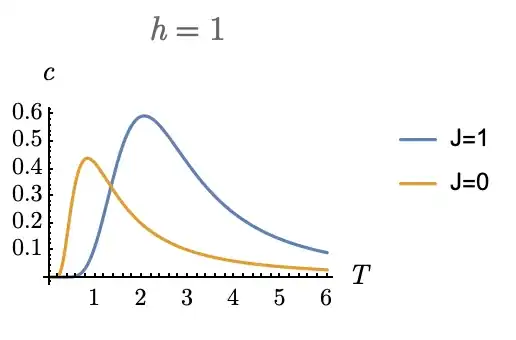
I made some plots for 1d Ising chain with finite N, and it seems like there is always a maximum of specific heat and susceptibility at certain temperature. As the N gets larger and larger, the maximum moves to T=0. We know there is no phase transition in 1d Ising model, then what the temperatures of maximum of specific heat and susceptibility correspond to? I attach some plots below for 4 spins Ising chain with periodic boundary condition. enter image description here

enter image description here

enter image description here

enter image description here

lol
  • 503

1 Answers1

1

This behavior is expected, and it's due to the finite-size scaling. You will see the same behavior for 2D case as well. As you make the system larger, your results will get closer to what you expect from analytical solution. After all, analytical solutions are derived for infinite chains/lattices. No wonder if a small scale lattice can't simulate their behavior completely. And because of this, we tend to use Monte Carlo or other methods for large enough lattices.

check this for example: http://physics.bu.edu/~py502/slides/l17.pdf

Paradoxy
  • 1,320
  • 9
  • 15
  • I disagree with this answer. The Schottky anomaly in the specific heat is present present in system of all sizes: it is not a finite-size effect. In fact, the $J=0$ case of the OP corresponds to independent spins, so the number of spins is completely irrelevant (apart from a trivial linear scaling of the specific heat by $N$). – Yvan Velenik Jan 18 '20 at 07:50
  • @YvanVelenik I am not sure what do you mean, in the case of $J=0$ we would still have $\mu\sum h_i S_i$ term, which of course depends on spins. If we remove this term as well, everything will become zero at all temperatures. Surely Schottky anomaly can explain the behaviour of Ising model, but OP is asking why does critical temperature go to smaller value as number of spins increases. And we know that 1d ising model doesn't have phase transition. – Paradoxy Jan 18 '20 at 09:34
  • Sure. But this is not the case for the specific heat: the peak does not disappear. So its presence is not due to any finite-size effect at all. Of course, the presence of this peak is not at all a signature of a phase transition in the model. – Yvan Velenik Jan 18 '20 at 09:45
  • 1
    And my comment regarding the number of spins is that, when $J=0$, everything reduces to a single spin problem (the number of spins yields only a trivial factor $N$). This shows that, in this case, the presence of the peak in the specific heat does not tend to $0$ as $N$ tends to infinity: changing the number of spins only scales the function by a factor of $N$, the position of the peak is unaffected. – Yvan Velenik Jan 18 '20 at 09:46
  • @YvanVelenik I see, well you are completely right about "the presence of the peak is not a signature of phase transition" but I didn't mean that "the presence of peak is due to the finite size effect" either. I was trying to say, "as N becomes larger the peak moves toward smaller values of temperature, and it's due to the finite size effect" and of course as you pointed out correctly, this is not the case for $J=0$. So if OP is asking why there is a peak anyway, your answer is correct. If he is asking why peak moves toward smaller values (while $J>0$) then it'd because of finite size effect. – Paradoxy Jan 18 '20 at 14:31
  • Yes (but I'd stress that, for the specific heat, the peak does not move to zero in the thermodynamic limit even when $J\neq 0$.). In any case, unfortunately, what kind of answers the OP is expecting is unclear... – Yvan Velenik Jan 18 '20 at 15:55
  • @YvanVelenik I was looking for your answer. Thanks a lot! – lol Jan 18 '20 at 21:07
  • @lol : Good, then! Happy it helped. :) – Yvan Velenik Jan 19 '20 at 09:00