If we can't see a real inverted image without the help of a screen, why are we able to see an inverted image on the concave side of a spoon and in the convex lens when the object is far from the focal point?
-
In books it's been printed so – Mithun Nov 07 '19 at 12:57
-
See this questions – M. Enns Nov 07 '19 at 13:11
-
thanks there buddy couldn't give answer to mine – Mithun Nov 07 '19 at 13:24
-
You can see a real image without a screen as explained in this answer to the question Real images and their formation. – Farcher Nov 07 '19 at 13:35
2 Answers
I was intrigued by the statement "If we can't see a real inverted image without the help of a screen ...". I think we can see a real inverted image without the help of the screen, as long as we position ourselves carefully and correctly, and this is what happens when we use an ordinary telescope. I will explain the situation using a sequence of diagrams.
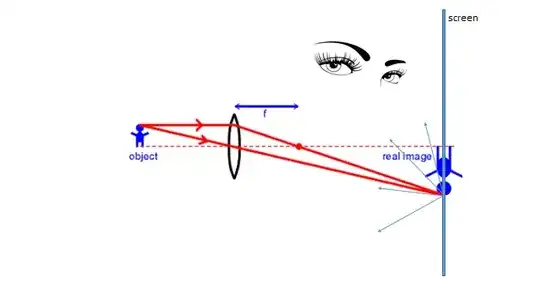
Here is a situation where a real inverted image has been formed, but the viewer does not see it:
Here the viewer (indicated by the pair of eyes) does not see the image simply because no light is propagating in the direction from the image towards the viewer's eyes.
Here is what happens when we put a screen in:
The screen scatters the light in all directions. Consequently, some goes towards the viewer's eyes and consequently the viewer can see the image. The screen also helps the viewer to focus their eyes on the correct spot.
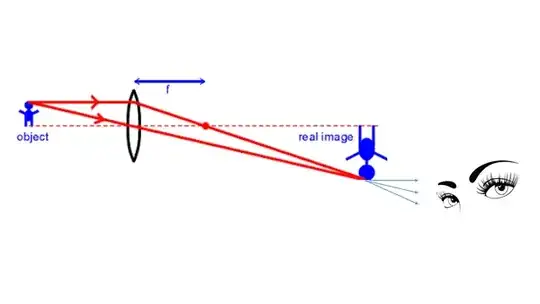
Finally, here is the situation with no screen but the viewer located in a spot from where they can see the image:
In this case the viewer can certainly see the image, but they may have trouble focusing their eyes on it. To help with this, one could try to eliminate light coming from other places, and perhaps provide the viewer with a magnifying glass or eye-piece. This is exactly what happens in an ordinary refracting telescope:
(This diagram shows a telescope focused at infinity, but essentially the same result applies for a telescope focused on an object at some large but finite distance, producing a real image at the little arrow labelled $h$).
- 58,183
This is a figure from Hewitt's Conceptual Physics of how one sees oneself in a concave mirror:
If one would be beyond the center of curvature, one would see oneself upside down (and at the center, one's eye fills the whole spherical mirror).
Similar for objects behind the viewer, but it is a bit more difficult to do the raytracing. For a large experiment, see for example this video from the Exploratorium or this one from Freiburg.
-
To show that one has an image, one must trace more than one ray propagating from each point on the object, in order to discover whether those rays converge to another point (the image point), and to locate the image point if they do. – Andrew Steane Feb 01 '21 at 10:17
-
@AndrewSteane The focusing is done in the eye. This illustration shows how the angular magnification comes about. – Feb 01 '21 at 12:10
-
True, but the diagram shows an image (a virtual image) on the right of the reflecting surface. One cannot deduce that there is a virtual image there if one only traces one ray per point. We want the idea that all the light rays from a single point on the hat, say, all appear to have come from a single point on the virtual image. – Andrew Steane Feb 01 '21 at 12:23
-
@AndrewSteane It does not matter where the constructed image is, at larger distances it is a real inverted image behind one's head. That is not what one sees. – Feb 01 '21 at 12:44