What does the magnitude of centripetal acceleration actually represents?

Question

A fan moving with an angular velocity of 5π rad/second has a centripetal acceleration of 175.185 m/s^2.The Centripetal acceleration doesnt express the change in velocity as it is constant. Then what does 175.185 m/s^2 actually represents?

Answer 1

Velocity measures speed and direction.

Although magnitude of velocity stays the same, it's direction is constantly changing. A change in the direction of velocity is a change in velocity; which requires an acceleration. This would be the centripetal acceleration in this case.

I guess it's worth noting that you're only given the magnitude of the acceleration as well. The direction of the acceleration also changes with the movement, so although it has a constant magnitude, it is not actually constant either.

Answer 2

It means change of the magnitude of the perpendicular/radial/centripetal velocity component.

The parallel velocity component is constant. And the perpendicular one is zero. Pull perpendicularly to cause a perpendicular acceleration, and the velocity will achieve a perpendicular component.

But in the very moment this perpendicular component should appear, the velocity vector turns, so the perpendicular direction changes and remain zero.

In other words, this perpendicular acceleration pulls in the object and causes it to move sideways, but only momentarily, instantaneously, for an infinitely short moment. So short that only turning has time to happen, but not speed up.

Answer 3

You have to remember that velocity and acceleration are vector quantities. The acceleration vector describes how the velocity vector changes over time. In other words, if our object has a velocity described by a vector vector at some time $\mathbf v(t_0)$ and is subject to an acceleration $\mathbf a$, then after a short time $\Delta t$ the new velocity is. $$\mathbf v(t_0+\Delta t)=\mathbf v(t_0)+\Delta t\cdot\mathbf a$$

Velocity has units of distance per time, so $\Delta t\cdot\mathbf a$ must also have the units of distance per time. $\Delta t\cdot\mathbf a$ is a vector of magnitude $\Delta t\cdot |\mathbf a|$ that points in the direction of $\mathbf a$. It is the vector you add to the velocity vector to find your new velocity vector.

The number you get of $175.185\ \mathrm{m/s^2}$ is the value of $|\mathbf a|$. The direction of the acceleration vector changes with time, but we can describe it as, for example $$\hat a=-\cos(\omega t)\hat i-sin(\omega t)\hat j$$ where $\omega$, for example, is your $5\pi\,\mathrm{rad/s}$. Then the acceleration vector is
$$\mathbf a=(175.185\ \mathrm{m/s^2})\cdot[-\cos(5\pi t)\hat i-\sin(5\pi t)\hat j]$$

Answer 4

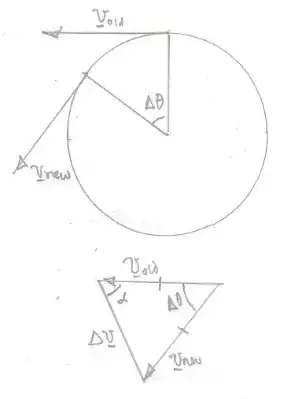
Suppose that there is an object moving at constant speed $v$ in a circle.

In a time $\Delta t$ the velocity of the object changes from $\vec v_{\rm old}$ to $\vec v_{\rm new}$ as shown in the diagram below.

A velocity vector triangle can be drawn showing that $\vec v_{\rm old}+ \Delta \vec v = \vec v_{\rm new}$.

As $\Delta t \to 0$ so $\Delta \theta \to 0$ and $\alpha \to 90^\circ$ so the direction of the change in velocity is towards the centre of the circle.

As $\Delta t$ becomes closer and closer to $0$ then the magnitude of the change in velocity, $\Delta \vec v$, becomes closer and closer to $175.185 \,\Delta t$ where $175.185 \,\rm m\,s^{-2}$ is the magnitude of the centripetal acceleration.

Answer 5

In addition to the previous answers:

The precise value, $175.185 \text{ m/s} ^2$ is the linear acceleration of any point on the fan blade exactly $0.71$ metres from the axis of rotation, if any such point exists.

The formula for centripetal acceleration is:$$a=\omega ^2r=\frac{v^2}{r}$$where

$a$ = the linear acceleration. in $\text{ metre/second} ^2$, of a point moving in a circle;

$\omega$ = the angular velocity in radians per second;

$v$ = the linear velocity of the point, in metres/second;

$r$ = the radius of the circle the point is moving in

Since $a$ and $\omega$ are given, the value of $r$ can be calculated.

If we assume a $1$ gram mass ($.001$ kg) is attached to the fan blade at this particular radius, Newton's Second Law requires a force be applied to the mass:$$F = ma =0.1758 \text{ Newtons}$$

If the blade is not strong enough to supply this tension force, the blade will fail and the mass will fly off in a straight line.