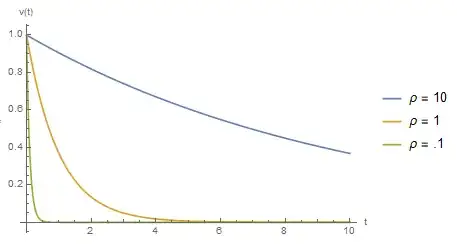
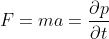1

If you horizontally throw a sphere of radius $R$ it will feel, in this direction, a drag force due to air. Assume the drag is given by Stokes law, $F_D=6\pi\eta R v$, where $\eta$ is the air viscosity and $v$ is the horizontal speed. This force cannot "see" the internal structure of a toy balloon, a football or even a metal sphere. However, anyone who ever played with balls and toy balloons noticed that for the same throwing, the ball will have higher horizontal reach for the same time interval. Just think about someone kicking toy balloons and footballs and the distances reached in each case. How is the resistive force considerably greater for the toy balloon?

Even if we consider a quadratic drag, $bv^2$, I suppose the coefficient $b$ would depend only on the fluid and the geometry of the bodies. Again the drag would be equal.

Another way to put this question: How does the density of the sphere contribute for the resistive force?

Diracology
  • 17,700
  • 3
  • 54
  • 97

4 Answers4

6

For a balloon and a football (soccer ball for Americans) of the same size, shape, and initial velocity, the aerodynamic drag will be the same. The effect on the motion of these objects will be very different because of their different masses. A football has a mass of about 0.430 kg while a balloon has a mass of less than 0.010 kg--1/40 of the football. This means that the balloon will decelerate 40x faster than the football.

Mark H
  • 24,002
5

Let's say you get your object to some initial speed $v$ and then let it go so that only the drag force is acting on it (ignoring gravity for now).

Then by Newton's second law: $$a=\frac{F_D}{m}=\frac{F_D}{\rho V}=\frac 1\rho \cdot \frac {F_D}{V}$$

Where $\rho$ is the density of the object. Since $\frac {F_D}{V}$ depends on the velocity and the geometry, then for two objects with the same geometry and same initial velocity, the object with the smaller density will have the larger acceleration due to the drag force.

We can even use your case to get the velocity as a function of time: $$\frac{dv}{dt}=-\frac{6\pi \eta R}{\rho V}v(t)$$ $$v(t)=v_0Exp\left (-\frac{6\pi \eta R}{\rho V}t\right)$$

Comparing different plots for various values of $\rho$ gives us something like this:

enter image description here

As you can see, smaller density leads to a faster decrease in velocity.

So your thoughts are correct. The force itself does not care about the insides of the object, only the outer cross section that influences the drag. However, as you can see, this means that more dense objects, which have more inertia (mass), are less effected by this drag force.

BioPhysicist
  • 56,248
3

Given about the same size of a balloon and a football, the main difference in how far they advance horizontally is their kinetic energies, not air resistance.

Since the velocity of an arm is limited, the initial velocity of a balloon would be similar to the initial velocity of a football and, since the football is much heavier, its kinetic energy will be much greater and it'll take much longer to lose (going against air resistance) than for the balloon.

The reason a balloon appears to have greater air resistance than a football is because air resistance is a dominant force that has to be overcome when throwing a balloon, while the dominant force for a football goes against its "inertial resistance", i.e., is used to speed up its mass.

So, for the football, air resistance represents a small faction of the total "resistance" and, therefore, is almost imperceptible.

V.F.
  • 12,193
3

We know that

Where p=mv is the momentum.

If both the balloon and the ball initialy have the same speed when you throw them, then the ball will have more momemtum than the balloon because it is more massive (p =mv).

So that if the force of friction on both of them is the same, the rate of change of momentum is the same. But since the momentum of the balloon is very small, it's momentum will go to zero faster.

Maxter
  • 546