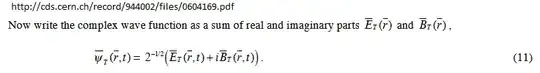0

An aerial reacts to EMR: to the electric or magnetic field of the radiation according to its orientation with respect to the transmitter, right? now,

  • what is the ratio of a photon's electric to its magnetic field strength? and,
  • what is the value of a photon's electric field with regard to an electron's electric field strength? Does it vary with its frequency?

EDIT : in my comments

user157860
  • 681
  • Possible duplicate of Amplitude of an electromagnetic wave containing a single photon – John Rennie Feb 02 '18 at 06:51
  • @JohnRennie, can we compare a photon in a box to a radio signal at an aerial? the radio wave is made up of photons of fairly similar frequency , so I thought is an ideal situation. The answers to the question you link are contrasting, my question is more specific, anyway: ratio e/B of the photon and ratio between the e fields of a photon and an electron and, lastly if it is dependent on frequency – user157860 Feb 02 '18 at 07:08
  • 1
    The problem is that a photon is a surprisingly elusive beast. A light wave is not a hail of photons. The question I linked gets a precise answer because it specifies precisely what it means by a photon. – John Rennie Feb 02 '18 at 07:31
  • So I don't think your question has an answer unless you specify what you mean by a photon. Also it doesn't make much sense to compare the oscillating electric field of an EM wave to the static electric field of an electron. – John Rennie Feb 02 '18 at 07:33
  • @JohnRennie, a photon does have an electric field, it oscillates alright, but if you make an electron oscillate you get an oscillating electric field exactly similar to the field that makes the charges in an erial oscillate. The fact that this issue is elusive and tricky, doesn't mean the problem has to be swept under the carpet. Is the field strength of a medium wave equal to the strength of a short wave or a microwave? whatever you think a photon or a wave is, that is certainly a clear and legitimate question – user157860 Feb 02 '18 at 07:40
  • @JohnRennie, take one electron and make it oscillate 10^9 times a second, an electromagnetic wave is produced, can we call it a photon? does it have an electric (oscillating) field? – user157860 Feb 02 '18 at 09:27
  • 2
    A photon does not have an electromagnetic field. A photon is the electromagnetic field. – safesphere Feb 02 '18 at 09:54
  • If you move an electron with an acceleration (e.g. "oscillate"), the electron (depending on conditions and the frame of reference) may emit an electromagnetic radiation described by a wave function. If you detect this radiation, it would manifest itself as photons. The energy and frequency of photons would depend on the acceleration, but not on the frequency, at which you oscillate the electron. For example, if you increase the amplitude at the same frequency, the frequency of photons will increase. The intensity will be the highest in turnaround points where the acceleration is higher. – safesphere Feb 02 '18 at 16:32
  • @safesphere, are you sure of that? do you have a link? doen't the frequency of the wave depend solely on the frequency of the oscillator? – user157860 Feb 05 '18 at 06:37
  • Oscillations are a special case of rotation. Let's rotate electrons for example. If we look at them in the plane of rotation, we would see them simply oscillationg. They would indeed emit electromagnetic waves or photons. According to you, the frequency of the wave should match the frequency of the oscillations or rotation. Consider a cyclotron where the speed is close to the speed of light. At 10 meters in diameter, the rotation is 10MHz. The typical emission is 14.4keV (around the Fe-57 absorption line) corresponding to 3.5 trillion MHertz. The quantum to clasical connection is complicated. – safesphere Feb 06 '18 at 05:48

1 Answers1

4

One has to keep in mind clearly what light is, i.e. classical electromagnetic radiation, and what a photon is : an quantum mechanical elementary particle of mass zero and spin 1.

Classical Maxwell's equation describe beautifully the behavior of light and electromagnetic radiation generally, including the behavior when em radiation hits an antenna.

The photons have a wavefunction given by solutions of a quantized Maxwell's equation, an example here

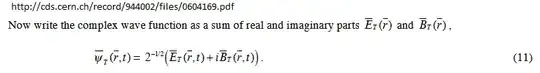
photw

Note the E and B in the wavefunction. These are the electric and magnetic fields of the classical wave which will emerge from zillions of photons with that E and B.

As E and B appear in the complex wavefunction a photon does not really have an electric or magnetic field, it just has the energy=h*nu where nu is the frequency of the classical wave to which this single photon can contribute. The probability of being located in space is given by the $Ψ*Ψ$ .

A photon interaction with matter, the antenna included, would involve the square of the wave function $Ψ*Ψ$, but the emergent beam comes from a superposition of photons, not interaction.

In analogy to thermodynamic quantities emerging from the underlying statistical mechanics, light emerges from the underlying photon level. This can be shown with quantum field theoretical calculations

With this in mind:

what is the ratio of a photon's electric to its magnetic field strength?

Similar to the classical field, but it is expressed in an imaginary complex space, not in four dimensional space

what is the value of a photon's electric field with regard to an electron's electric field strength?

As the square of the electric field of the classical beam is proportional to the energy of the beam, it means that many photons will add up to build up the classical electric field.

From the above, a single photon does not have an electric field to be compared with the free electric field of an electron. It is the emergent ensemble that has an electric field.

The image in this link may help for intuition .

photspin

Does it vary with its frequency?

A photon, if it is in a superposition of wave functions with other photons will have the same frequency since it can only lose energy with interactions, and its energy is = h*nu, nu is the frequency.

The underlying photon behavior is complex, and classical solutions are more than adequate for most situations .

anna v
  • 233,453
  • thanks, all being equal, power of transmitter, aerial etc, what is the difference of the strength of the electric field of a medium/short/ micro wave? – user157860 Feb 02 '18 at 09:22
  • To reduce it to very simple words, the common picture of a single photon absorbed by oscillator in term of their Elec. fields oscillating in resonance is meaningless? I.e. would be better to say that the energy of the photon fits with an oscillator level and that is. Can I say so? – Alchimista Feb 02 '18 at 09:43
  • @Alchimista an antenna works with the emergent electric field from a great number of photons, this classical size electric field is the one the electrons in the conduction band are attracted and repulsed to, and thus transmit a signal/current for further processing. Antennas work with metals only, the conduction bands. The photons will end up in scattering coherently off, or losing energy becoming thermal, but the signal comes from the variations of the emergent classical E field as the em arrives on the antenna. – anna v Feb 02 '18 at 12:32
  • as for relative strenght it will depend on what the source can provide. The strength is proportional to E^2, so the more power the higher the field, the frequency does not play a role to first order., except as for the size of the generating antenna – anna v Feb 02 '18 at 12:35
  • Thanks Anna. I was/am not concerned what antennas and anything ib which the EM wave is a collection of photons. Really at down scale, e.g. an oscillating molecular dipole associated to vibration Shall we stop with the photon seeing as a " wobbling sperm" carring an E field resonating with the absorber? Or in other words how to link the energy hf to that of the electrical field ? This question and the OP question are recurrent here but I couldn't find an easy answer if not seeing by the eyes of the absorber (I manage some QM). So the point is not what the absorber can take, but how a single. – Alchimista Feb 02 '18 at 13:05
  • ....... how a single photon goes through space. Is it an EM maxwellian wave with the minimum energy possible (for that frequency) or not? This is not answered by taking it as a quantum wave, or perhaps it is associating the E field according to the probability to find it at a given xyz and t. But it is not the typical EM depiction. All my concern originates from the assumption that a single photon can travel and be absorbed. – Alchimista Feb 02 '18 at 13:12
  • Ps: if it sounds not too clear please consider I am on mobile . I must learn how to go to chat as for time and space as well as dynamical discussion might help when treating not very simple arguments :) – Alchimista Feb 02 '18 at 13:33
  • The accepted answer here https://physics.stackexchange.com/questions/47105/amplitude-of-an-electromagnetic-wave-containing-a-single-photon seems to mitigate my discomfort :) I will go through it more carefully – Alchimista Feb 02 '18 at 13:38
  • @Alchimista that answer is really semiclassical. I am answering trying to explain that the photons as represented in quantum field theory by creation and annihilation operators, build up the classical fields in a complex superposition. The second image I have linked for how macroscopic polarizstion is connected with the photon spin, shows that the photons spin -1 builds richt handed polarization, while the +1 left handed, even though the electric field is going all around for the classical polarization. It is not mathematically simple. – anna v Feb 02 '18 at 15:51
  • Thanks. This is basically as to say that a single photon cannot be treated/depicted as an EM wave. And its absorption to be described as superposition of states not by equally oscillating electricmag fields. – Alchimista Feb 02 '18 at 15:58