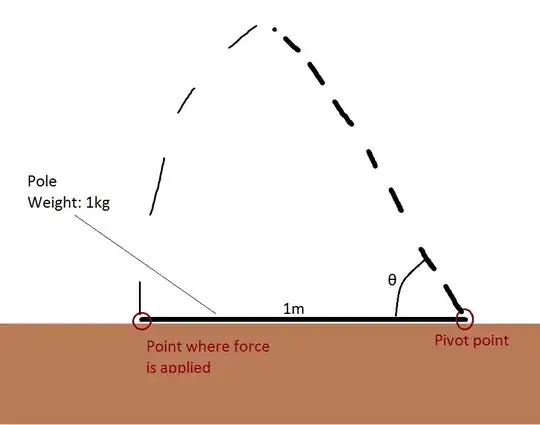
What would be the function for work done in order to raise the pole by an angle θ, as illustrated? I know that at flat ground, the force needed to lift the pole is about (m/2)×9.81, but I assume this changes as more weight is held by the pivot point as it rises?
Edit: So that makes sense, since the center of mass will be closer to the pivot point, as the angle goes towards 90 degrees.
Since the L×F = d×m, where L is the length from where the force is applied to the pivot point, F is the force needed, d is the distance from the pivot point to the centre of mass, and m is the mass of the object (in this example the pole), we can rearrange it to this: F = (d×m)/L
Since we are lifting from the edge, length of pole = 1m = L
d = cos(θ)×(1/2)×L which means
F(θ) = (cos(θ)×(1/2)×L×m)/L = cos(θ)×(1/2)×m
So if I assume correctly, the Work done would just be an integration of this function going from 0 degrees to θ?
∫cos(θ)×(1/2)×m dx = (1/2)×sin(θ)×m = Work?