A metal (or otherwise, suitably elastic) circle is cut and the points are slid up and down a vertical axis as shown:
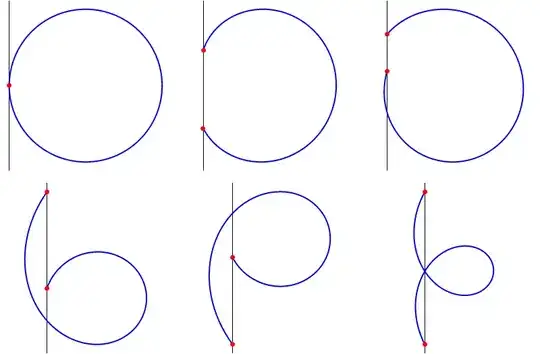
How would one describe the resultant curves mathematically?
A metal (or otherwise, suitably elastic) circle is cut and the points are slid up and down a vertical axis as shown:

How would one describe the resultant curves mathematically?
This problem was first formulated by Leonhard Euler in 1744 WPlink: "That among all curves of the same length which not only pass through the points A and B, but are also tangent to given straight lines at these points, that curve be determined in which minimizes the value of \begin{equation} \int_A^B \frac{ds}{R^2} \end{equation}
It is a problem of calculus of variations and the Euler-Lagrange equations WPlink allows to solve it as an ODE of the type:
\begin{equation} \frac{dy}{dx} = \frac{a^2 - c^2 + x^2}{\sqrt{(c^2 - x^2)(2a^2 - c^2 + x^2)}} \end{equation}
The physical meaning is this: the wire will take the shape that minimizes the total energy related to bending further in each point. This energy is similar to the the spring potential energy for deformations, but in this case the measure of the deformation is the curvature $k = \frac{1}{R}$. Since in your proposal, the elastic line was initially a circle, I would propose the integral to be: \begin{equation} \int_A^B (\frac{1}{R} - k_0)^2ds \end{equation} where $k_0$ would be the initial curvature which should be the rest one. I would set it constant here since for the circle it is the same in any point, but in general if you start with a different rest position, the rest curvature in each point will differ from point to point.
Now let's analyze the curves, and group them. If we number them from left to right and from top to bottom we can make the 2 following groups:
Fixed ends condition: The curves 1,2 and 6. This curves are only determined by fixating the extremes of the curve, or frontier conditions. This means that they are shapes that the curves will take naturally under no external forces on any point of it.
Fixed ends + one fixed end angle conditions: The curves 3,4 and 5. It can be seen that 4 and 5 are the same. This curves need, apart from the fixed extremes condition, the fixing of one or two of the extremes' angle. A bending force there or some general external force acting on one r more points of it would cause them as well. If they did not have this extra condition, nothing would prevent them from falling back to form 2 or 6.
Finally, here is a review of the solutions, with a great historical presentation of the problem: ElasticaHistory. But if you really want to get serious I recommend A Treatise on the Mathematical Theory of Elasticity.