5

What is the relationship between the focal length and field of view for an equal-area ("equisolid") projection fisheye lens? Alternatively, what is the relationship between the 180-degree image circle size and the focal length for such a lens?

Ultimately I want to find the field of view of a Tokina 10-17 mm fisheye zoom at focal lengths other than 10 mm on APS-C (at 10 mm Tokina claims 180 degrees diagonally).

mattdm
  • 143,140
  • 52
  • 417
  • 741
Szabolcs
  • 2,883
  • 2
  • 24
  • 38

2 Answers2

4

Michel Thoby's webpage has the following formula for the equal-area projection:

r = 2 f sin(θ/2)

where r is the distance from the centre in the projection plane of a point that is visible under angle θ.


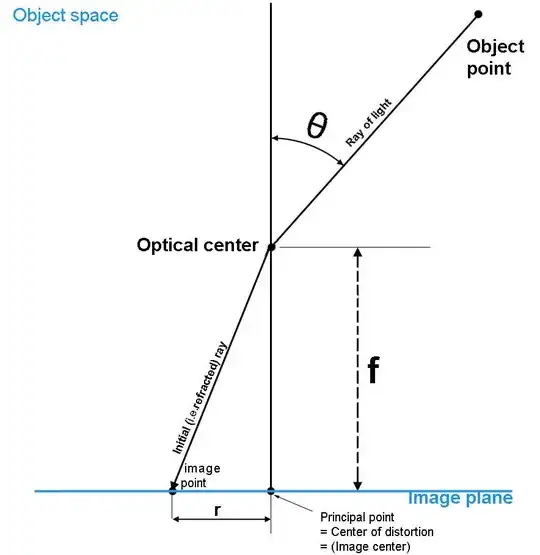
(image source)

For 10 mm focal length this gives r = 2 * 10 mm * sin(π/2 / 2) = 14 mm for the radius of the 180-degree image circle. This roughly matches the half diagonal of APS-C sensors (nominally 15 mm). Diagonal fisheye lenses using this projection indeed all have ~ 10 mm focal length (Nikon 10.5 mm, Sigma 10 mm, Tokina 10-17 mm).

The reverse formula for calculating the field of view will be

FoV = 2 θ = arcsin(r / (2f))

where r is now the half-diagonal of the sensor. For APS-C with r = 15 mm and f = 17 mm this gives 105 degrees, which matches Tokina's claim for 100 degrees at 17 mm.

We can also make a plot to show the field of view versus focal length for equal area projection fisheyes, and compare with rectilinear lenses.

enter image description here

Most current APS-C cameras have slightly smaller sensors with diagonals closer to 14 mm, so in practice the angle of view will be a bit less than what's shown on this graph. Let's make another plot for the sensor size of an actual camera (Nikon D7100).

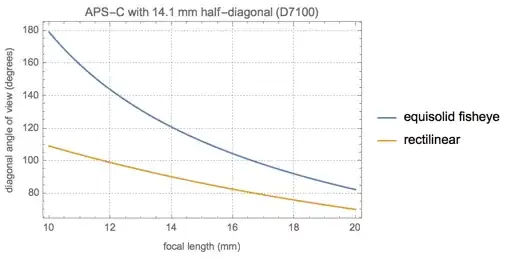
enter image description here

Note 1: This is not valid for all fisheye lenses. Some use different projections, such as the Samyang 8 mm, which is said to be closer to stereographic. The page linked above has a lot of information on various projections.

Note 2: Some projection software such as PanoTools use a more general projection formula of r = k1 f sin(θ/k2) where k1 and k2 are found empirically (from measurements) for different lenses. This page shows the results of such measurements.

Originally I made a mistake and forgot the one half factor from the sine function, which caused a wrong result and confused me. Instead of deleting the question I'm posting this as community wiki anyway as others may find it useful.

Mr.Wizard
  • 416
  • 4
  • 17
Szabolcs
  • 2,883
  • 2
  • 24
  • 38
  • Why make this answer CW? It's a perfectly valid answer, and with a little editing, the original question itself is a good one. I couldn't find another question here that exactly applied. I say un-CW the answer, and get your well-deserved rep – scottbb Apr 26 '16 at 13:29
  • @scottbb Well, yesterday I made an embarrassing mistake when I forgot that 1/2 factor from inside of the sine (see my comment on the other answer). If I had found that mistake earlier, I would have deleted the question ... I was worried about backlash. I don't care much about reputation score any more, so CW is okay. – Szabolcs Apr 26 '16 at 13:43
  • What formula are you using for the rectilinear lens? The projection mapping function is image height = focal length * tan (angle off axis) Your rectilinear curve looks mostly, well, linear, and it should be blowing up starting around 80 degrees. The formula image height = focal length * (angle off axis) is not the formula for a rectilinear lens, but is the formula "weak fisheyes" use. – Brandon Dube Apr 26 '16 at 17:08
  • @Brandon The inverse of what you mentioned: 2 arctan(r/f), where r = 15 mm is the half-diagonal of APS-C. – Szabolcs Apr 26 '16 at 18:18
  • 1
    Here is another page that covers these formulas: http://www.bobatkins.com/photography/technical/field_of_view.html – Mr.Wizard Oct 24 '19 at 09:53
-1

The angle of view calculation requires trigonometry: This is the formula I use in Excel.

=((ATAN((d/2/f)))x180/9.8596

d=the dimension of the frame 35mm full frame 24mm height by 36mm length diagonal 42.36mm f=focal length x=multiply

10mm = 100⁰ height – 121⁰ length 127⁰ diagonal

12mm = 90⁰ height – 113⁰ length 120⁰ diagonal

14mm = 81⁰ height – 104⁰ length 114⁰ diagonal

17mm = 70⁰ height – 93⁰ length 104⁰ diagonal

For the compact (APS-C) 16mm height by 24mm length by 30mm diagonal

10mm = 77⁰ height – 100⁰ length 110⁰ diagonal

12mm = 67⁰ height – 90⁰ length 100⁰ diagonal

14mm = 60⁰ height – 81⁰ length 82⁰ diagonal

17mm = 50⁰ height –70⁰ length 81⁰ diagonal

Alan Marcus
  • 39,160
  • 3
  • 48
  • 91
  • 1
    What you wrote is valid for a rectilinear lens, i.e. for projection through a point. It also needs a factor of 2 in front of the arc-tangent. But this is not a rectilinear lens, far from it. Hence my question. – Szabolcs Apr 25 '16 at 19:33
  • Then I don't know the math sorry! – Alan Marcus Apr 25 '16 at 19:42
  • I found this page which claims that the distance r for a point from the image centre is r = 2*f*sin(θ/2), where f is the focal length and θ is angle measures from the optical axis for that point. But it doesn't add up. Equal-area projection lenses that have a 180 degree diagonal FoV tend to have ~10 mm focal length (like this Tokina or the Nikon 10.5 mm). According to this formula they'd have a 20 mm radius 180 deg image circle. But the half-diagonal of APS-C is only 15 mm... – Szabolcs Apr 25 '16 at 20:10