There are two hard limits on how fast a lens can be:
The first is a thermodynamic limit. If you could make a lens arbitrarily fast, then you could point it to the sun and use it to heat your sensor (not a good idea). If you then get your sensor hotter than the surface of the Sun, you are violating the second law of thermodynamics.
This sets a hard limit at f/0.5, which can be derived from the conservation of etendue. Well, technically it's more like T/0.5. You can make lenses with f-numbers smaller than 0.5, but they will not be as fast as their f-numbers suggest: either they will work only at macro distances (with “effective” f-numbers larger than 0.5), or they will be so aberrated as to be useless for photography (like some lenses used to focus laser beams, which can only reliably focus a point at infinity on axis).
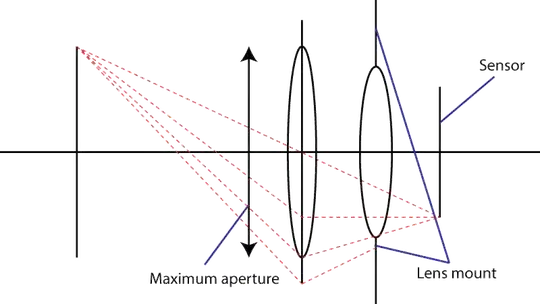
The second limit is the mount. This limits the angle of the light cone hitting the sensor. Your trick of using a diverging element dos not work. You certainly get a wider entrance pupil, but then you have a lens combination which has a longer focal length than the initial lens. Actually, your trick is very popular: it’s called a “telephoto” design. Bigger lens, same f-number.
If the lens mount allows for a maximum angle α for the light cone, then the fastest lens you can get will have an f-number equal to
$$
\begin{align}
N &= \frac{1}{2\sin\left({\alpha\over 2}\right)} \\
&= {1\over 2\,\mathrm{NA}}
\end{align}
$$
where NA is the numerical aperture. This formula also shows the hard limit at 0.5: sin(α/2) cannot be larger than 1. Oh, BTW, if you try to derive this formula using small-angle approximations, you will get a tangent instead of a sine. Small-angle approximations are not good for very fast lenses: you should use the Abbe sine condition instead.
The same caveat about f-numbers v.s. T-numbers applies to this second limit. You can get a lens with an f-number smaller than 1/(2×sin(α/2)), but it will work as macro-only, and the bellows-corrected f-number will still be larger than the limit.
Derivation
This section is intended for the mathematically inclined. Feel free to ignore it, as the relevant results are already stated above.
Here I assume that we use a lossless lens (i.e. it conserves luminance) to focus the light of an object of uniform luminance \$L\$ into an image plane. The lens is surrounded by air (index 1), and we look at the light falling on an infinitesimal area \$\mathrm{d}S\$ about, and perpendicular to, the optical axis. This light lies inside a cone of opening \$\alpha\$. We want to compute the illuminance delivered by the lens on \$\mathrm{d}S\$.
In the figure below, the marginal rays, in green, define the light cone with opening α, while the chief rays, in red, define the target area \$\mathrm{d}S\$.

(source: edgar-bonet.org)
The etendue of the light beam illuminating \$\mathrm{d}S\$ is
$$
\mathrm{d}G = \mathrm{d}S\int\cos\theta\,\mathrm{d}\omega
$$
where \$\mathrm{d}\omega\$ is an infinitesimal solid angle, and the integral is over \$\theta\in[0, \alpha/2]\$. The integral can be computed as
$$\begin{align}
\mathrm{d}G &= \mathrm{d}S \int 2\pi \cos\theta\sin\theta\,\mathrm{d}\theta \\
&= \mathrm{d}S \int\pi\,\mathrm{d}\!\left(\sin^2\theta\right) \\
&= \mathrm{d}S \,\pi \sin^2\left({\alpha\over 2}\right)
\end{align}$$
The illuminance at the image plane is then
$$
I = L\,\frac{\mathrm{d}G}{\mathrm{d}S} = L\,\pi\sin^2\left({\alpha\over 2}\right)
$$
We may now define the “speed” of the lens as its ability to provide image-plane illuminance for a given object luminance, i.e.
$$
\text{speed} = {I\over L} = \frac{\mathrm{d}G}{\mathrm{d}S} = \pi\sin^2\left({\alpha\over 2}\right)
$$
It is worth noting that this result is quite general, as it does not rely on any assumptions about the imaging qualities of the lens, whether it is focused, aberrated, its optical formula, focal length, f-number, subject distance, etc.
Now I add some extra assumptions that are useful for having a meaningful notion of f-number: I assume that this is a good imaging lens of focal length \$f\$, f-number \$N\$ and entrance pupil diameter \$p = f/N\$. The object is at infinity and the image plane is the focal plane. Then, the infinitesimal area \$\mathrm{d}S\$ on the image plane is conjugated with an infinitesimal portion of the object having a solid-angular size \$\mathrm{d}\Omega = \mathrm{d}S/f^2\$.
Given that the area of the entrance pupil is \$\pi\left({p\over 2}\right)^2 = {\pi\over 4}p^2\$, the etendue can be computed on the object side as
$$\begin{align}
\mathrm{d}G &= \mathrm{d}\Omega\,\frac{\pi p^2}{4} \\
&= \mathrm{d}S\,\frac{\pi p^2}{4f^2} \\
&= \mathrm{d}S\,\frac{\pi}{4N^2}
\end{align}$$
And thus, the speed of the lens is
$$
\text{speed} = {\mathrm{d}G\over \mathrm{d}S} = \frac{\pi}{4N^2}
$$
Equating this with the speed computed on the image side yields
$$\begin{align}
\require{cancel}
\frac{\cancel{\pi}}{4N^2} &= \cancel{\pi} \sin^2\left({\alpha\over 2}\right) \\
N^2 &= \frac{1}{4\sin^2\left({\alpha\over 2}\right)} \\
N &= \frac{1}{2\sin\left({\alpha\over 2}\right)}
\end{align}$$
I should insist here on the fact that the last assumptions I made (the lens is a proper imaging lens focused at infinity) are only needed for relating the speed to the f-number. They are not needed for relating the speed to sin(α/2). Thus, there is always a hard limit on how fast a lens can be, whereas the f-number is only limited insofar as it is a meaningful way of measuring the lens’s speed.


N = 1/(2 sin(\alpha/2)))? 2) What are typical values of \alpha on common camera mounts? – Unapiedra Nov 24 '14 at 19:03