How to test actual focal length?

Question

From Matt Grum's comment to my previous question, I learned that manufacturers may casually "round" actual focal length of a lens to some nice number that gets printed on the box and stored into EXIF. From his answer to the same question, it seems I would need to know actual focal length of a lens to test what aperture is used.

I have also heard that most lens will change focal length when focused very close.

How would I go about testing what focal length my lens is actually using when focused on a given distance? EXIF obviously won't help me here, because data is put there by manufacturer.

Answer 1

There is a mathematical / measurement method to calculate the effective focal length of a lens by measuring its angle of view.

The formula for angle of view is given as

$$ \alpha = 2\arctan{d\over2f} \qquad[1]$$

To calculate effective focal length \$f\$, rearranging equation 1 comes down to:

$$\begin{align} f &= {d\over 2\tan(\alpha/ 2)} \\ &= {d\over 2}\cot\left({\alpha\over 2}\right) \end{align}$$

where \$d\$ represents the size of the sensor in the direction measured. \$d\$ would be 24 mm in case you are using a full frame camera.

Let us now have the following setup for measuring \$\alpha\$;

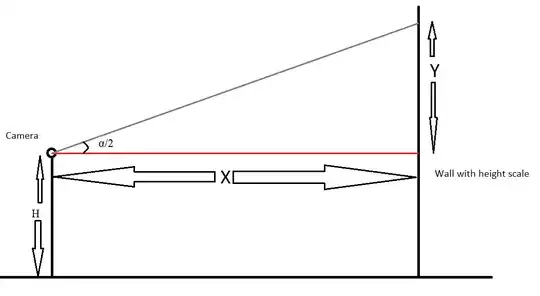
You have a camera sitting at a height \$H\$ from the ground and a distance of \$X\$ from the wall with a scale. Now take a picture and you should be able to read the maximum height the lens can see (this would be \$H + Y\$).

Now knowing \$X\$ and \$Y\$, we can calculate half the angle of view (i.e. \$\alpha/2\$) using a right-triangle calculator (\$X\$ would be the opposite side and \$Y\$ the adjacent side), which uses the formula

$$ {\alpha\over 2} = \arctan{Y\over X} $$

Now that you have figured out \$\alpha/2\$, use it on equation 1 to calculate the effective focal length of the lens.

The value is only accurate as your measurements.

Edit 1:
In reference to @mattdm’s comment: Are the manufacturer-stated sensor dimensions close enough?

With reference to sensor sizes of camera’s in these links: here and here, we can logically assume that camera makers or at least Canon and Nikon round their sensor sizes 1/10 of an mm; i.e. there is a possibility of ±0.05 mm error in case they round the sensor size.

Let us consider 3 type of lenses:

1. Wide angle lens (say 13 mm, angle of view: 85.4º)
2. Normal lens (50 mm, angle of view 27.0º)
3. Telephoto lens (300 mm, angle of view: 4.58º)

The effect of a 0.05 mm change in sensor size are:

change for wide Angle lens = 0.05 / (2 * tan(85.4/2)) = 0.04613 mm appx.
Which represents an difference of 0.35% (i.e. (0.04613 / 13) * 100 )

change for normal lens= 0.05 / (2 * tan(27/2)) = 0.012 mm appx.
Which represents an difference of 0.024% (i.e. (0.012/ 50) * 100 )

change for telephoto lens= 0.05 / (2 * tan(4.58/2)) = 0.0019 mm appx.
Which represents an difference of 0.0006% (i.e. (0.0019/ 300) * 100 )

We can thus see that with a 13mm wide angle lens and taking a 0.05mm error in manufacturers’ measurement, the change in the focal length is only 0.35%.

I hope that my math is correct.

Edit 2:
Regarding measurements for \$X\$ and \$H\$,

• \$H\$ should be measured from ground to the horizontal center of the sensor.
• \$X\$ is the distance between sensor and the wall.

Answer 2

Assuming a standard lens, standard camera, i.e. the setup can be modelled as a pin-hole camera. This doesn't work with tilt/shift, and maybe not with wide-angle lenses (if you want to know about those, we could work it out).

In computer vision, often the intrinsic properties of cameras are calculated. Intrinsic because they refer to settings of the camera within the camera. Extrinsic properties are orientation and position. Intrinsic properties are several, among them the magnification. My solution is:

• Use a standard tool from Computer Vision (CV) to calibrate the camera and lens at the given settings.
• Look up the pixel size for your camera.
• Ask someone else to convert magnification to focal length. (I don't know yet how this works)

Calibration

Calibrating in CV is mostly done using a chess board pattern. You take several (~10) photos of that pattern from various positions and distances. The algorithm works then in the following way:

Pretend that you know the position of each vertice on the board, find a set of parameters to the camera model that best explain seeing all the points on the board in the images.

In theory I would recommend OpenCV for this, it has an example code for that. But this is maybe not too practical (you'll need to install OpenCV for this, and possibly change a bit of code.). There are probably other solutions out there that do this.

Calculating focal length

The result of the calibration step is the K matrix (called the intrinsic matrix). It maps 3-space points in the camera's coordinate system to homogeneous 2-space points on the image plane. (Multiple View Geometry, p. 157, 2nd Ed, 2003, Hartley & Zisserman)

$$ K = \begin{bmatrix} \alpha & 0 & p_x \\ 0 & \alpha & p_y \\ 0 & 0 & 1 \end{bmatrix} $$

We only care about \$\alpha\$ here. \$p_x\$ is about half the sensor width in pixels, similarly for \$p_y\$, it relates to where the principal ray intersects the image plane. Interestingly my cheap phone camera violates that much more than a good DSLR, or even an expensive webcam, or an iPhone 4 camera.

\$\alpha\$ is then related to the focal length: $$\alpha = f m$$

• \$m\$ is the number of pixels per unit distance in image coordinates.
• \$f\$ is the focal length.

But note: this is in the pinhole camera model, so the distance between image plane and pinhole of the camera. I am not sure how to find the focal length photographers think of to it.

Alternative

Someone posted a link about a different approach, "Measuring Focal Length" at BobAtkins.com

Under the heading "The Easy Way" in the article a different method is proposed. Given two stars, look up the positions of the stars and calculate the angle between them. Then see how your camera setup measures that angle. Read the link for a complete run-through.

The downside of that is that it won't work with any focal distance but only focus at infinity. On the other hand, my approach won't work at infinity. Or treat 500 m as infinity, buy a corn field and mow a chess board pattern into it, rent plane and take photos from 500m up...

Answer 3

Calculate the magnification M of the lens using the object and image size. With M and the object distance the focal length of the lens may be calculated.

As an example. I image a two meter (\$S_o\$) stick which is 10 meters (\$d_o\$) from the camera. From the image the 2 m stick is 1000 pixels wide. Each pixel is 10 µm giving a image size of 0.01 meters (\$S_i\$). The magnification is $$ M = {S_i\over S_o} = {0.01\over 2} = 0.005 $$

I think with $$ M = {f \over f-d_o} $$ you can calculate the focal length \$f\$. (You might want to confirm with an optics book.)

Answer 4

I looked at Bob Atkins' "Easy method", but it leaves you to work some astro data out.

My version of his method provides all the astro how-to info and links, with step-by-step instructions, and should be significantly easier for novices to implement.

http://www.pentaxforums.com/forums/pentax-lens-articles/169225-using-2-stars-determine-actual-focal-length-lens-distance.html

Answer 5

You can set the lens on a rest like a book thus making a crude optical bench. Well illuminate a target. Best is a ruler. Adjust the lens so the image of the ruler falls on a white paper screen.

Fiddle with the distances until the image of the ruler is “life-size”. You know, 1:1 otherwise called “magnification one”. Using another ruler, measure the distance between markings on the image of the projected rule. Using two identical rulers helps. Now establish the necessary 1:1 magnification.

Now measure the distance between target and screen. Divide this value by 4. This answer gives the focal length of the lens.