Assume for a moment that I wanted to take photographs with my SRL with no lens attached. Suppose that I wanted to get extremely blurry, mostly solid color photographs. How would I set the camera's shutter speed to achieve a "proper exposure" of my blurry field of average tones. What Fstop is no lens?
Don't worry about my sensor, in this thought experiment it's a 35mm film camera.
You can use pinhole camera calculations. It doesn't really matter that it is a terribly made/designed pinhole camera.
The distance that the lens mount opening (pinhole lens) is in front of the image/film plane is the camera's focal length. And the opening's diameter in relation to the focal length is it's f-ratio/f#. For the Nikon F mount SLR/DSLR's w/o a lens it is 46.5mm flange distance ÷ 44mm lens mount opening = f/1.06
Of course, you still need a measure of the light intensity, and know the film's sensitivity, in order to determine an appropriate SS (at least approximately).
Imagine the point of view of one of the center-most point of the film or sensor plane, looking out of the camera box: your viewport of the world is the angle of view that is limited by the camera's flange. As it turns out, there's a fundamental concept in optics called the numerical aperture, a dimensionless number that characterizes that acceptance angle:
N.A. = n sin(),
where n is the index of refraction of the material, and is the half-angle of the acceptance angle (it makes things easier for most of optics to measure from the optical axis, rather than the total acceptance angle). Since there is no lens, and the sensor is in air, then we can assume n = 1, so the N.A. is simply sin().
Rather than measuring with a protractor, we can just calculate it from basic trigonometry, since we know the diameter of the camera's flange (D) and its distance from the sensor (f):
= atan(D / 2 f)
Putting it all together,
N.A. = sin(atan(D / 2 f)) (again, assuming n = 1)
Note that in the case of no lens attached, there isn't really a "focal length", because it's completely afocal. In this case, f is still the distance to the aperture though.
When talking about refractive optics, and also with pinhole cameras without refractive optics, we often define the f-number as N = f / D. But understand that definition only holds within the paraxial approximation, wherein sin() ≈ tan() ≈ . That is, it only holds for small . For pinhole cameras, D is usually very small (hence the name 'pinhole'), so sine and arctangent essentially become inverse functions of each other, and thus sin(atan(D / 2 f)) = D / 2 f = N.A.
But that just means that the f-number N = 1 / (2 N.A.). As it turns out, that's actually the definition of f-number.
So let's calculate some "f-numbers" for various camera without lenses attached:
| Camera mount | flange diameter D | flange distance f | N.A. | N |
|---|---|---|---|---|
| Nikon F | 44 mm | 46.5 | 0.428 | 1.17 |
| Pentax K | 44 mm | 45.46 mm | 0.436 | 1.15 |
| Canon EF | 54 mm | 44 mm | 0.523 | 0.96 |
| Sony E | 43.6 mm | 18 mm | 0.771 | 0.65 |
| Canon RF | 50.6 mm | 20 mm | 0.784 | 0.64 |
| Nikon Z | 52 mm | 16 mm | 0.852 | 0.59 |
| naked sensor, no body | ∞ | 0 | 1 | 0.5 |
Take note of that last line in the table: for a "camera" with no body (i.e., no throat limiting the angle of view of the sensor), sort of the "degenerate case" of the system, the half acceptance angle is 90º (the result of atan(∞/0)), which is the argument angle for which the sine function produces its maximum value, 1.
Thus, the maximum N.A. for an optical system in air (n = 1) is 1, and the corresponding fastest/widest theoretical f-number for any photographic system in air is f = 0.5.
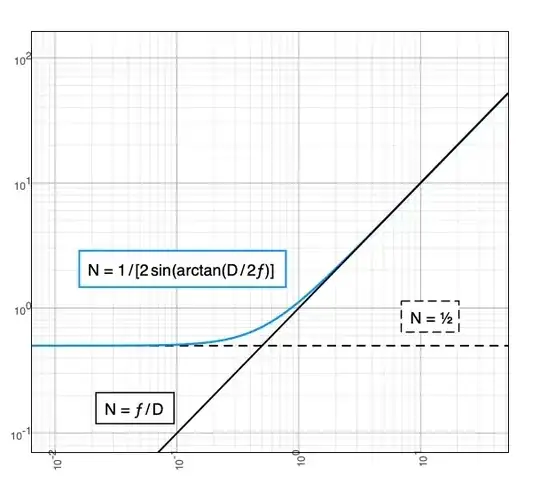
In the log-log graph below, the horizontal axis x is the ratio f / D. The 3 functions are:
The solid blue line clearly aysmptotes to 0.5 as its argument gets small (that is, as D / f gets large, either because of a short focal length, or arbitrarily large throat diameter).
Another way to think of F-stop is in terms of Light Reduction. A fast f/1.4 lens is 1-stop down or half the light (1/(1.4)^2) of an f/1.0. An f/0.9 lens would be (1/(0.9)^2)) or 1.23 times more light.
No lens would be zero effect on light levels, corresponding to f/1.0.
Many years ago I did take some pictures with No Lens. I was using a Minolta SRT-303 (European number for a U.S. 102). I believe, but am no longer sure, that the camera builtin metering defaulted to its maximum aperture of F/1.0 (There was an f/1.2 lens available so it had to handle at least that). Setting the shutter for correct exposure seemed to work.
So why would anyone want to take pictures without a lens?
I had some early attempts at astro-photograpy, specifically Saturn and Jupiter on Kodachrome-64. I didn't have access to an enlarger capable of doing the kind of massive blowup I wanted to try. In lieu of a super-enlarger, I put the original in a slide projector and projected directly onto the Minolta with no lens.
It worked! Getting the film plane aligned with the projector focus was ... painful ... but the end result was a super enlargement, along with horrid grain and crazy contrast, but it worked.
My suggestion is try F/1.0 and bracket.
